From a sphere of mass M and radius R, a smaller sphere of radius R2 is carved out such that the cavity made in the original sphere is between its centre and the periphery (see figure. ) for the configuration in the figure where the distance between the centre of the original sphere and the removed sphere is 3R, the gravitational force between the two sphere is :
(##DSH_NTA_JEE_MN_PHY_C07_E01_012_Q01.png" width="80%">
41GM23600R2
41GM2450R2
59GM2450R2
GM2225R2
The correct Answer is:A
To solve the problem, we need to find the gravitational force between the original sphere of mass M and radius R and the smaller sphere carved out of it, which has a radius of R2. The distance between the centers of the two spheres is given as 3R.
1. Calculate the Mass of the Carved Sphere:
The volume of the original sphere is given by:
V=43πR3
The mass density ρ of the original sphere is:
ρ=MV=M43πR3=3M4πR3
The volume of the smaller sphere (carved out) with radius R2 is:
Vsmall=43π(R2)3=43πR38=16πR3
The mass m of the carved sphere is:
m=ρ⋅Vsmall=3M4πR3⋅16πR3=M8
2. Calculate the Gravitational Force:
The gravitational force F between two masses M1 and M2 separated by a distance r is given by Newton's law of gravitation:
F=GM1M2r2
Here, M1=M (mass of the original sphere) and M2=m=M8 (mass of the carved sphere). The distance r between their centers is 3R.
Substituting the values:
F=GM⋅M8(3R)2=GM28⋅9R2=GM272R2
3. Adjust for the Effect of the Carved Sphere:
The gravitational force exerted by the carved-out sphere on the original sphere must be subtracted from the total gravitational force. The distance from the center of the carved sphere to the center of the original sphere is 3R−R2=5R2.
The gravitational force due to the carved sphere on the original sphere is:
Fcarved=G⋅M8⋅M(5R2)2=G⋅M2825R24=GM250R2
4. Net Gravitational Force:
The net gravitational force between the two spheres is:
Fnet=F−Fcarved=GM272R2−GM250R2
To combine these, we need a common denominator, which is 3600R2:
Fnet=GM272R2⋅5050−GM250R2⋅7272
=GM2⋅503600R2−GM2⋅723600R2=GM2(50−72)3600R2=−22GM23600R2
Since we are looking for the absolute value of the force:
Fnet=22GM23600R2
5. Final Result:
The final gravitational force between the two spheres is:
Fnet=41GM23600R2
Conclusion:
The gravitational force between the two spheres is:
41GM23600R2
The volume of the original sphere is given by:
V=43πR3
The mass density ρ of the original sphere is:
ρ=MV=M43πR3=3M4πR3
The volume of the smaller sphere (carved out) with radius R2 is:
Vsmall=43π(R2)3=43πR38=16πR3
The mass m of the carved sphere is:
m=ρ⋅Vsmall=3M4πR3⋅16πR3=M8
The gravitational force F between two masses M1 and M2 separated by a distance r is given by Newton's law of gravitation:
F=GM1M2r2
Here, M1=M (mass of the original sphere) and M2=m=M8 (mass of the carved sphere). The distance r between their centers is 3R.
F=GM⋅M8(3R)2=GM28⋅9R2=GM272R2
The gravitational force exerted by the carved-out sphere on the original sphere must be subtracted from the total gravitational force. The distance from the center of the carved sphere to the center of the original sphere is 3R−R2=5R2.
Fcarved=G⋅M8⋅M(5R2)2=G⋅M2825R24=GM250R2
The net gravitational force between the two spheres is:
Fnet=F−Fcarved=GM272R2−GM250R2
To combine these, we need a common denominator, which is 3600R2:
Fnet=GM272R2⋅5050−GM250R2⋅7272
=GM2⋅503600R2−GM2⋅723600R2=GM2(50−72)3600R2=−22GM23600R2
Fnet=22GM23600R2
The final gravitational force between the two spheres is:
Fnet=41GM23600R2
The gravitational force between the two spheres is:
41GM23600R2
Topper's Solved these Questions
- GRAVITATIONBook:DISHA PUBLICATIONChapter:GRAVITATIONExercise:EXERCISE -1
Explore 60 Videos
- GRAVITATIONBook:DISHA PUBLICATIONChapter:GRAVITATIONExercise:EXERCISE-2
Explore 30 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:DISHA PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:EXERCISE 2: CONCEPT APPLICATOR
Explore 24 Videos
- JEE MAINS- 2019 (HELD ON :9TH APRIL 2019 (SHIFT-I))Book:DISHA PUBLICATIONChapter:JEE MAINS- 2019 (HELD ON :9TH APRIL 2019 (SHIFT-I))Exercise:QUESTIONS
Explore 30 Videos
Similar Questions
From a solid sphere of mass M and radius R, a solid sphere of radius R/2 is removed as shown. Find gravitational force on mass m as shown

View Solutionfind the gravitational force of attraction between a uniform sphere of mass M and a uniform rod of length L and mass m, placed such that r is the distance between the centre of the sphere and the near end of the road.
View Solution
Knowledge Check
Inside a uniform sphere of mass M and radius R, a cavity of radius R/3, is made in the sphere as shown :
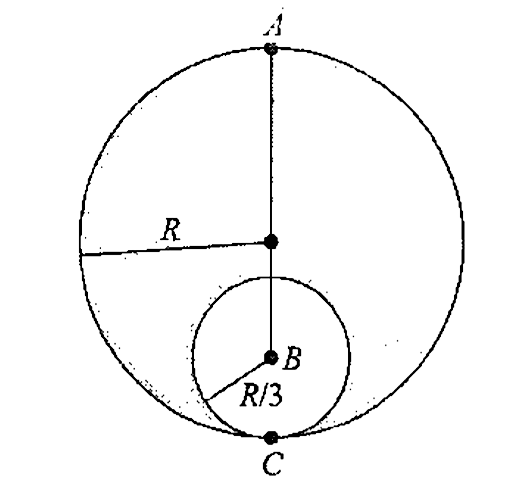 AGravitational field inside the cavity is uniformBGravitational field inside the cavity is non-uniformCThe escape velocity of a particle projected from point A is √88GM15RDEscape velocity is defined for earth and particle system only
AGravitational field inside the cavity is uniformBGravitational field inside the cavity is non-uniformCThe escape velocity of a particle projected from point A is √88GM15RDEscape velocity is defined for earth and particle system onlyTwo metal spheres each of radius r are kept in contact with each other. If d is the density of the material of the sphere,then the gravitational force between those spheres is proportional to
Ad2r6Bd2r4Cd2r4Dr2d2A solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distance R/4 from the centre of sphere. The gravitational force on mass m is
A11GMmR2B14GMmR2CGMm2R2DGMmR2
Two spheres each of mass M and radius R are separated by a distance of r. The gravitational potential at the midpoint of the line joining the centres of the spheres is
View SolutionAn insulating solid sphere of the radius R is charged in a non - uniform manner such that the volume charge density ρ=Ar, where A is a positive constant and r is the distance from the centre. The potential difference between the centre and surface of the sphere is
View SolutionAn insulating solid sphere of the radius R is charged in a non - uniform manner such that the volume charge density ρ=Ar, where A is a positive constant and r is the distance from the centre. The potential difference between the centre and surface of the sphere is
View SolutionA hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . Then y -coordinate of the centre of mass of the remaining sphere is

View SolutionThe radius of gyration of a solid sphere of radius R about a certain axis is also equal to R. If r is the distance between the axis and the centre of the sphere, then r is equal to
View Solution