In order to simulate different values of g aspiring astronauts are put on a plane which dives in a parabola given by the equation x2=500y. Where x is horizontal, y is vertically upwards, both being measured in meter. The x-component of the velocity of the plane is constant throughout, and has the value of 360km/h. the effective g("g-force") experienced by an astronaut on the plane equals
4g
3g
g5
5g
The correct Answer is:D
Differentiating the equation of the curve w.r.t we get ,
2(dxdt)2=500×d2ydt2
or, d2ydt2=2×104500=4g. The effective .g. = 5g.
Topper's Solved these Questions
- GRAVITATIONBOOK - DISHA PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - EXERCISE -1
60 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - DISHA PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - EXERCISE 2: CONCEPT APPLICATOR
24 Videos
- JEE MAINS- 2019 (HELD ON :9TH APRIL 2019 (SHIFT-I))BOOK - DISHA PUBLICATIONCHAPTER - JEE MAINS- 2019 (HELD ON :9TH APRIL 2019 (SHIFT-I))EXERCISE - QUESTIONS
30 Videos
Similar Questions
Two graphs of the same projectile motion (in the x - y plane) projected from origin are shown in (Fig. 5 .10). X - axis is along horozontal direction and Y - axis is vertically upwards. Take g=10ms2
Find (i) The y component of initial velocity and
(ii) the X component of initial velocity.
 .
.
View SolutionA particle is moving in the xy plane on a sinusoidal course determined by y = A sin kx, where k and A are constants. The X component of the velocity of the particle is constant and is equal to v0 and the particle was at origin at time t=0. Find the magnitude of the acceleration of the particle when it is at point having x co ordinate x=π2k.
View Solution
Knowledge Check
Equation of trajectory of a projectile is given by y=−x2+10x where x and y are in meters and x is along horizontal and y is vericall y upward and particle is projeted from origin. Then : (g=10)m/s2
Ainitial velocity of particle is √505m/sBhorizontal range is 10mCmaximum height is 25mDangle of projection with horizontal is tan−1(5).Two graphs of the same projectile motion (in the xy-plane) projected from origin are shown. X-axis is along horizontal direction and y-axis is vertically upwards. Take g=10ms−2.
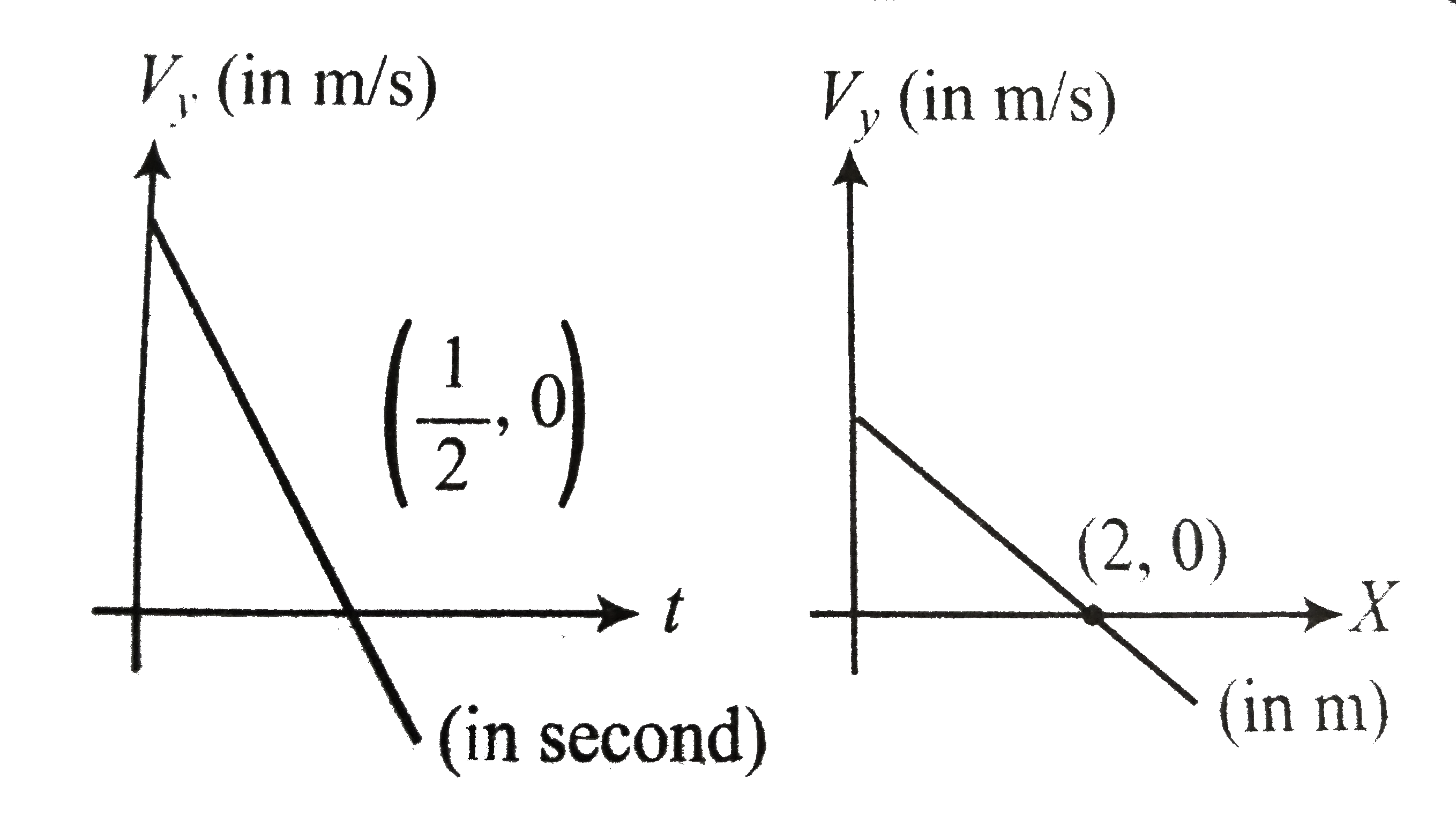 ,
,
The projection speed is :A√37ms−1B√41ms−1C√14ms−1D√40ms−1A body projected horizontally from the top of a tower follows y=20x2 parabola equation where x,y are in m(g=10m/s2).Then the velocity of the projectile is (ms−1)
A0.2B0.3C0.4D0.5
A ball thrown in air follows a path given by y=x√3−3g8x2m where x-axis is taken along the horizontal and y-axis along the vertical. The maximum displacement of the ball along x-direction for which displacement along y is zero equals to
View SolutionA point moves in xy-plane according to equation x = at, y = at (l - bt) where a and b are positive constants and t is time. The instant at which velocity vector is at π/4 with acceleration vector is given by:
View SolutionTwo graphs of the same projectile motion (in the xy-plane) projected from origin are shown. X-axis is along horizontal direction and y-axis is vertically upwards. Take g=10ms−2.
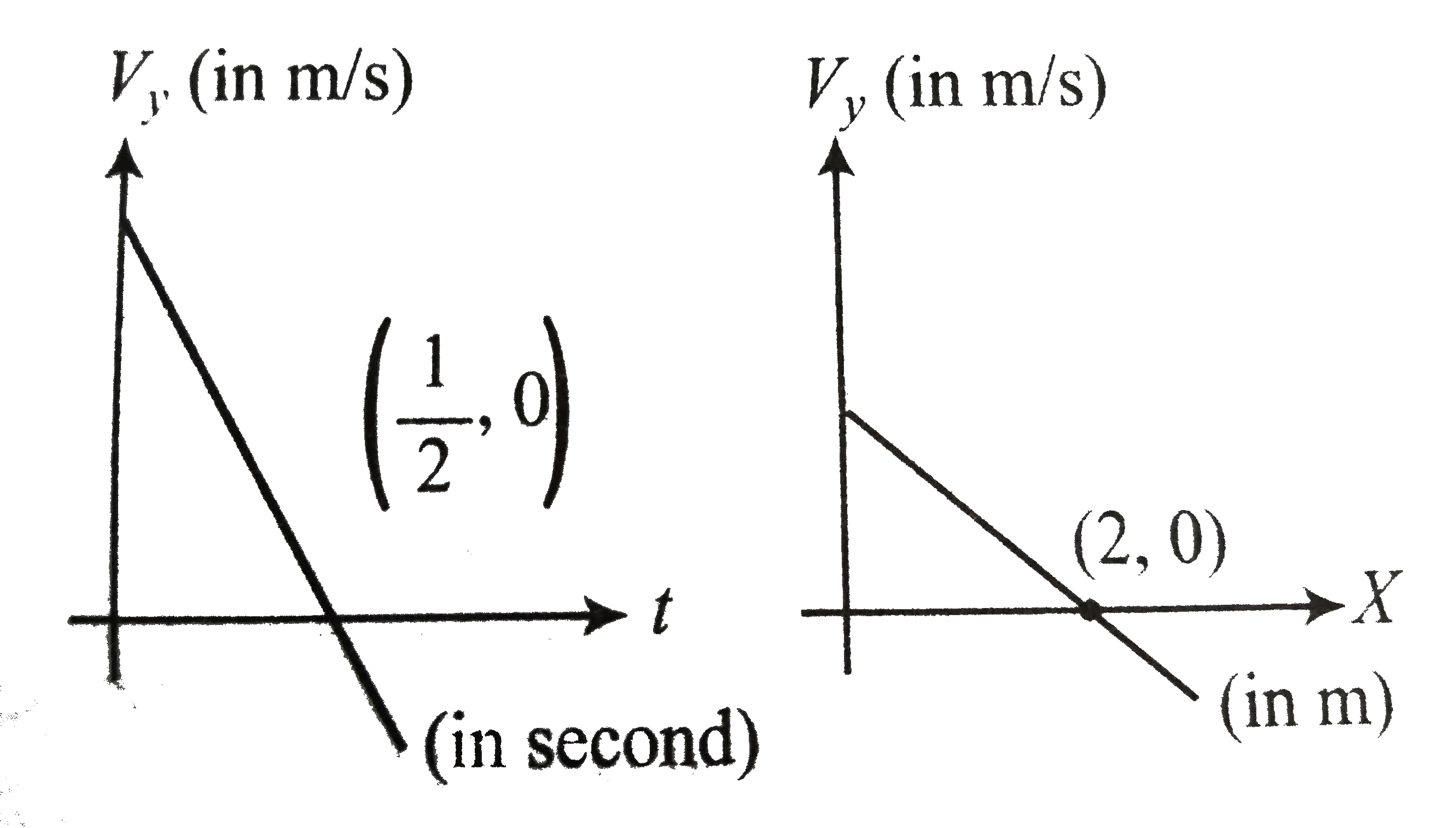 ,
,
Maximum height attained from the point of projection is
View SolutionTwo graphs of the same projectile motion (in the xy-plane) projected from origin are shown. X-axis is along horizontal direction and y-axis is vertically upwards. Take g=10ms−2.
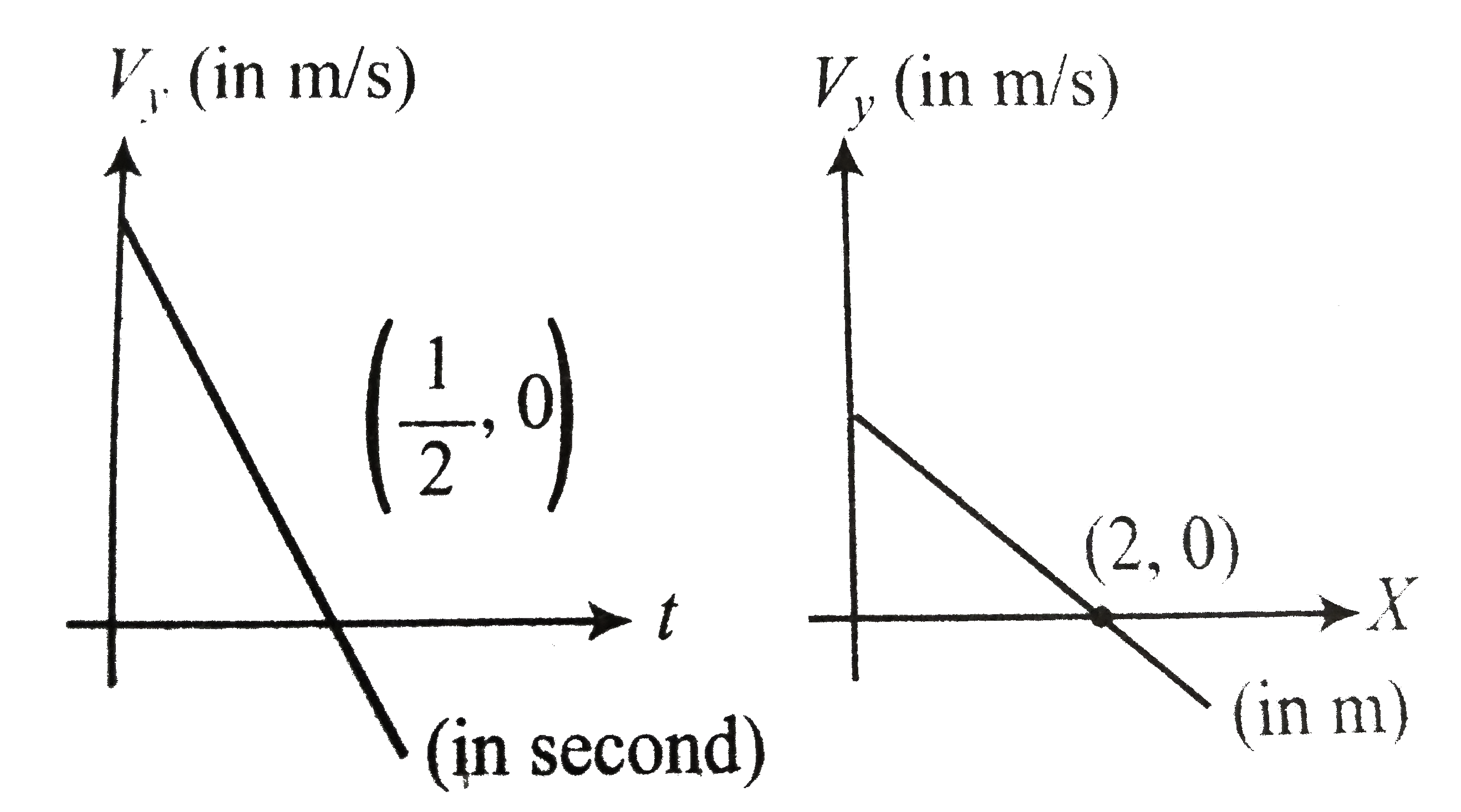
Projection angle with the horizontal is :
View SolutionAn particle is moving in xy - plane with a constant speed v0 such that its y displacement is given by
y=αe−(2vx√3v0), where vx is component of velocity along the x - axis. If at some instant x component of it velocity is positive and the slope of the tangent on its path is −1√3, then the displacement of the particle in y - direction at the instant is
View Solution
