From a solid sphere of mass M and radius R, a spherical portion of radiu R2 is removed as shown in the figure. Taking gravitational potential V = 0 at r=∞, the potential at the centre of the cavity thus formed is (G = gravitational constant)
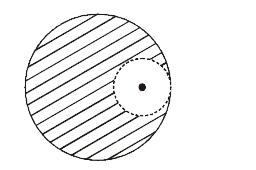
−2GM3R
−2GMR
−GM2R
−GMR
The correct Answer is:D
Step by step video, text & image solution for From a solid sphere of mass M and radius R, a spherical portion of radiu (R )/(2) is removed as shown in the figure. Taking gravitational potential V = 0 at r = oo, the potential at the centre of the cavity thus formed is (G = gravitational constant) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GRAVITATIONBOOK - DISHA PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - EXERCISE -1
60 Videos
- GRAVITATIONBOOK - DISHA PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - EXERCISE-2
30 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - DISHA PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - EXERCISE 2: CONCEPT APPLICATOR
24 Videos
- JEE MAINS- 2019 (HELD ON :9TH APRIL 2019 (SHIFT-I))BOOK - DISHA PUBLICATIONCHAPTER - JEE MAINS- 2019 (HELD ON :9TH APRIL 2019 (SHIFT-I))EXERCISE - QUESTIONS
30 Videos
Similar Questions
From a solid sphere of mass M and radius R, a solid sphere of radius R/2 is removed as shown. Find gravitational force on mass m as shown

View SolutionA sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.

View Solution
Knowledge Check
From a solid sphere of mass M and radius R, a spherical portion of radius R/2 is removed, as shown in the figure Taking gravitational potential V=0atr=∞, the potential at (G = gravitational constatn)
 A−2GM3RB−2GMRC−GM2RD−GMR
A−2GM3RB−2GMRC−GM2RD−GMRInside a uniform sphere of mass M and radius R, a cavity of radius R/3, is made in the sphere as shown :
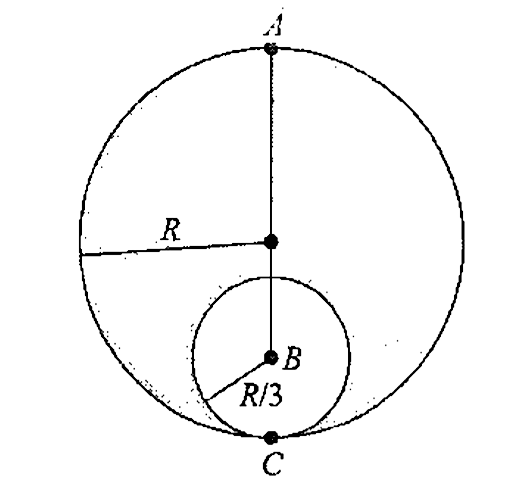 AGravitational field inside the cavity is uniformBGravitational field inside the cavity is non-uniformCThe escape velocity of a particle projected from point A is √88GM15RDEscape velocity is defined for earth and particle system only
AGravitational field inside the cavity is uniformBGravitational field inside the cavity is non-uniformCThe escape velocity of a particle projected from point A is √88GM15RDEscape velocity is defined for earth and particle system onlyFrom a solid sphere of mass M and radius R, a spherical portion of radius R2 is removed. The diameter of the cavity so formed coincides with a radius of the sphere. v0 was the escape speed of a particle projected from the surface of this sphere without cavity. Then the velocity v' that must be given to a particle along O Aso that it can just reach A, starting from within the cavity, is:
AV0Bv02Cv0√2Dv04
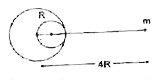
A particle of mass m is placed at a distance of 4R from the centre of a huge uniform sphere of mass M and radius R. A spherical cavity of diameter R is made in the sphere as shown in the figure. If the gravitational interaction potential energy of the system of mass m and the remaining sphere after making the cavity is λGMm28R. Find the value of λ
View SolutionThe correct variation of gravitational potential V with radius r measured from the centre of earth of radius R is given by
View SolutionA hemi-spherical cavity is created in solid sphere (of radius 2R) as shown in the figure. Then

View SolutionA shell of mass M and radius R has point mass m placed at a distance r from its centre. The gravitational potential energy U(r) vs r will be
View SolutionA spherical hole of radius R/2 is excavated from the asteroid of mass M as shown in the figure the gravitational acceleration at a point on the surface of the asteroid just above the excavation is

View Solution
