A particle is projected over a traingle from one end of a horizontal base and grazing the vertex falls on the other end of the base. If and be the base angles and the angle of projection, prove that .
The correct Answer is:B
For any point P (x,y),
we have
From figure ,
Hence ,

Topper's Solved these Questions
- MOTION IN A PLANE BOOK - DISHA PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Exercise -1 : CONCEPT BUILDER (TOPICWISE)
60 Videos
- MECHANICAL PROPERTIES OF FLUIDS BOOK - DISHA PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - EXERCISE-2 CONCEPT APPLICATOR
24 Videos
- MOTION IN A STRAIGHT LINEBOOK - DISHA PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Exercise-2
30 Videos
Similar Questions
A particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If αandβ be the base angles and θ the angle of projection, prove that tanθ=tanα+tanβ .
View SolutionA particle is projected over a triangle from one extremity of its horizontal base. Grazing over the vertex, it falls on the other extremity of the base. If aandb are the base angles of the triangle and θ the angle of projection, prove that tanθ=tan∝+tanβ.
View Solution
Knowledge Check
A particle is thrown over a triangle from one end of horizontal base and grazing over the vertex falls on the other end of the base. If α,β are the base angles and θ the angle of projection, then
Atanθ=tanα−tanβBtanθ=tanβ−tanαCtanθ=tanα+tanβDNone of theseA particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If 30∘and60∘ be the base angles and θ the angle of projection then tanθ is
A2√3B4√3C13D3If tanβ=cosθtanα, then tan2θ2=
Asin(α+β)sin(α−β)Bcos(α−β)cos(α+β)Csin(α−β)sin(α+β)Dcos(α+β)cos(α−β)
A particle thrown over a triangle from one end of a horizontal base falls on the other end of the base after grazing the vertex. If αandβ are the base angles of triangle and angle of projection is θ, then prove that (tanθ=tanα+tanβ)
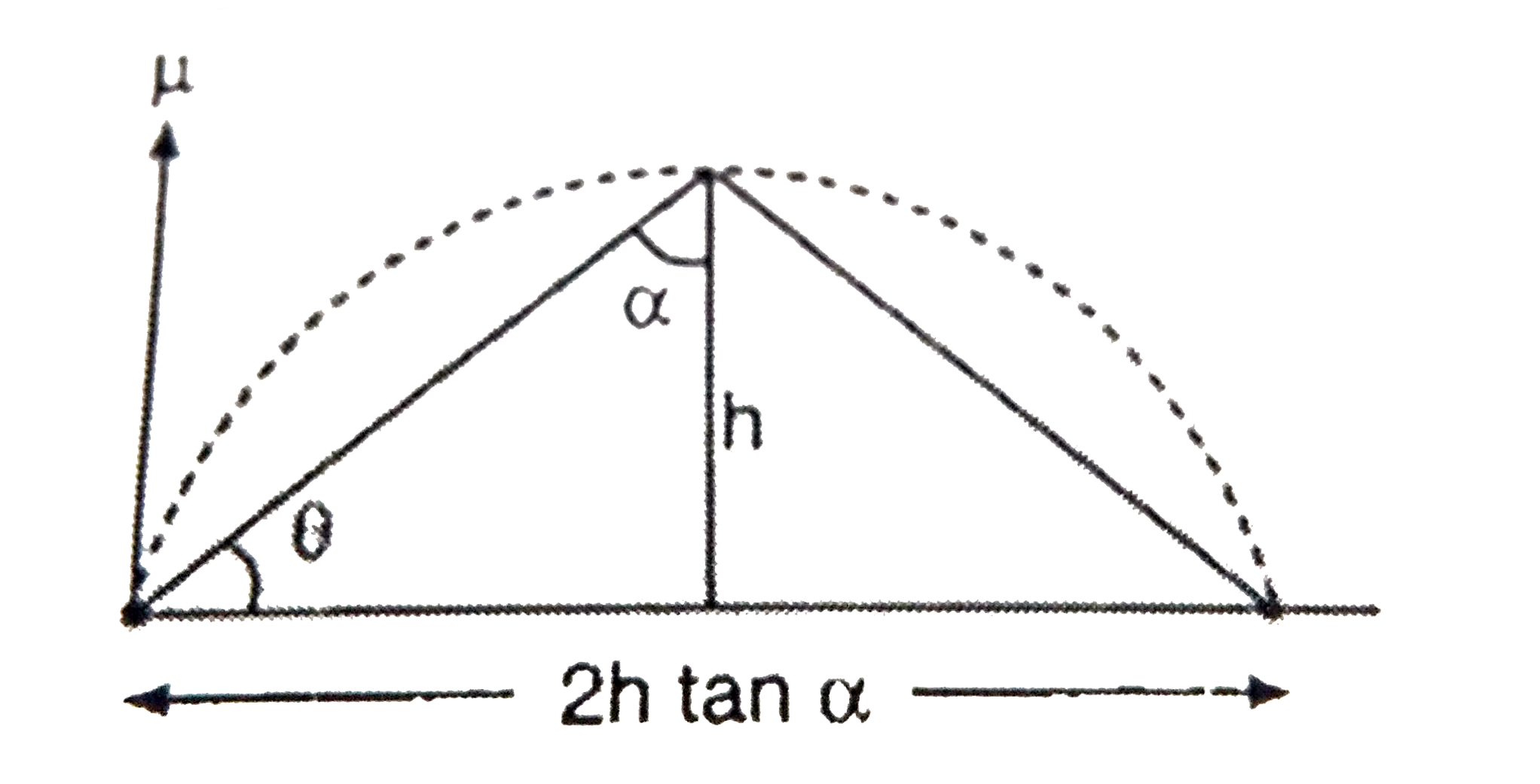
View SolutionA projectile is fired from the base of cone shaped hill. The projectle grazes the vertex and strikes the hill again at the base. If α be the half-angle of the cone, h its height, u the initial velocity of projection and θ angle of projection, then tanθtanα is:
View SolutionIf 2tanβ+cotβ=tanα , prove that cotβ=2tan(α−β).
View SolutionIf αandβ are roots of the equatioin acosθ+bsinθ=c, then find the value of tan(α+β).
View SolutionIf a cos2θ+bsin2θ=c has αandβ as its solution, then the value of tanα+tanβ is
View Solution
