What normal to the curve $y = x^{2}$ forms the shortest chord?

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $\sqrt{2} x - 2 y + 2 = 0; \sqrt{2} x + 2 y - 2 = 0$

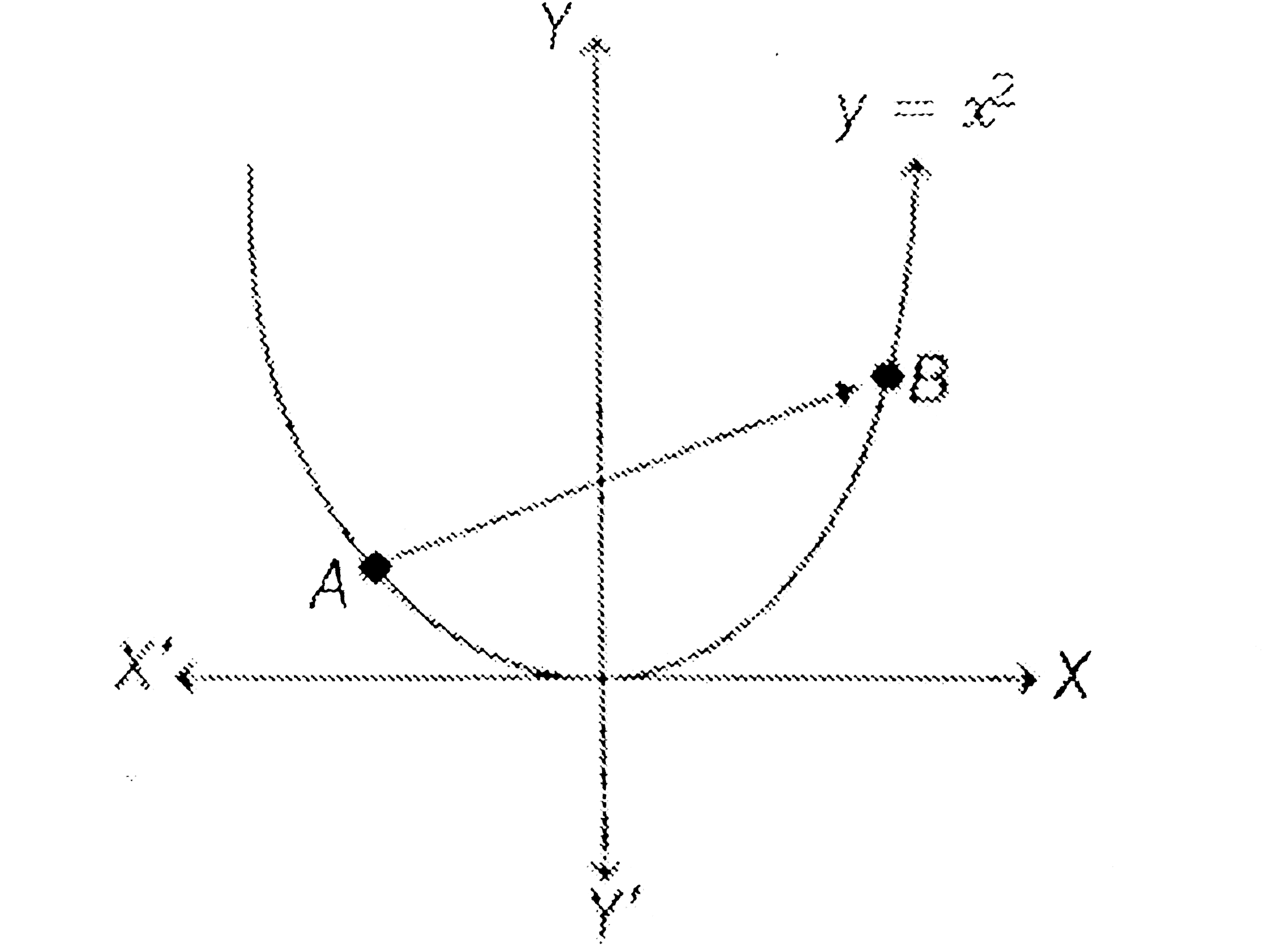
Any point on the parabola $y = x^{2}$ is of the form $(t, t^{2})$ .
Now, $\frac{d y}{d x} = 2 x \Rightarrow {[\frac{d y}{d x}]}_{x = t} = 2 t$
Which is the slope of the tangent. So, the slope of the normal to $y = x^{2}$ at $A (t, t^{2})$ is
$y - t^{2} = (- \frac{1}{2 t}) (x - t)$ ... (i)
Suppose Eq. (i) meets the curve again at $B (t_{1}, t_{1}^{2})$ .
Then, $t_{1}^{2} - t^{2} = - \frac{1}{2 t} (t_{1} - t)$
$\Rightarrow (t_{1} - t) (t_{1} + t) = - \frac{1}{2 t} (t_{1} - t)$
$\Rightarrow (t_{1} + t) = - \frac{1}{2 t}$
$\Rightarrow t_{1} = - t - \frac{1}{2 t}$
Therefore, length of chord,
$L = A B^{2} = {(t - t_{1})}_{1}^{2} + {(t^{2} - t_{1}^{2})}^{2}$
${(t - t_{1})}_{1}^{2} [1 + {(t + t_{1})}_{1}^{2}]$
$= {(t + t + \frac{1}{2 t})}^{2} [1 + {(t - t - \frac{1}{2 t})}^{2}]$
$\Rightarrow L = {(2 t + \frac{1}{2 t})}^{2} (1 + \frac{1}{4 t^{2}}) = 4 t^{2} {(1 + \frac{1}{4 t^{2}})}^{3}$
On differentiating w.r.t. t, we get
$\frac{d L}{d t} = 8 t {(1 + \frac{1}{4 t^{2}})}^{3} + 12 t^{2} {(1 + \frac{1}{4 t^{2}})}^{2} (- \frac{2}{4 t^{3}})$
$= 2 {(1 + \frac{1}{4 t^{2}})}^{2} [4 t (1 + \frac{1}{4 t^{2}}) - \frac{3}{t}]$
$= 2 {(1 + \frac{1}{4 t^{2}})}^{2} (4 t - \frac{2}{t}) = 4 {(1 + \frac{1}{4 t^{2}})}^{2} (2 t - \frac{1}{t})$
For maxima or minima, we must have $\frac{d L}{d t} = 0$
$\Rightarrow 2 t - \frac{1}{t} = 0 \Rightarrow t^{2} = \frac{1}{2}$
$\Rightarrow t = \pm \frac{1}{\sqrt{2}}$
Now, $\frac{d^{2} L}{{d t}^{2}} = 8 (1 + \frac{1}{4 t^{2}}) (- \frac{1}{2 t^{3}}) (2 t - \frac{1}{t}) + 4 {(1 + \frac{1}{4 t^{2}})}^{2} (2 + \frac{1}{t^{2}})$
$\Rightarrow {[\frac{d^{2} L}{{d t}^{2}}]}_{t = \pm 1 / \sqrt{2}} = 0 + 4 {(1 + \frac{1}{2})}^{2} (2 + 2) > 0$
Therefore, L is minimum, when $t = \pm 1 / \sqrt{2}$ . For $t = 1 / \sqrt{2}$ , point A is $(1 / \sqrt{2}, 1 / 2)$ and point B is $(- \sqrt{2}, \sqrt{2})$ . When $t = - 1 / \sqrt{2}$ , A is $(- 1 / \sqrt{2}, 1 / \sqrt{2})$ , B is $(\sqrt{2}, 2)$ .
Again, when $t = 1 e / \sqrt{2}$ , the equation of AB is
$\frac{y - 2}{\frac{1}{2} - 2} = \frac{x + \sqrt{2}}{\frac{1}{\sqrt{2}} + \sqrt{2}}$
$\Rightarrow (y - 2) {(\frac{1}{\sqrt{2}} + \sqrt{2})} = (x + \sqrt{2}) (\frac{1}{2} - 2)$
$\Rightarrow - 2 y + 4 = \sqrt{2} x + 2$
$\Rightarrow \sqrt{2} x + 2 y - 2 = 0$
and when $t = - 1 / \sqrt{2}$ , the equation of AB is
$\frac{y - 2}{\frac{1}{2} - 2} = \frac{x - \sqrt{2}}{- (\frac{1}{\sqrt{2}}) - \sqrt{2}}$
$\Rightarrow (y - 2) (- \frac{1}{\sqrt{2}} - \sqrt{2}) = (x - \sqrt{2}) (\frac{1}{2} - 2)$
$\Rightarrow 2 y - 4 = \sqrt{2} (x - \sqrt{2})$
$\Rightarrow \sqrt{2} x - 2 y + 2 = 0$

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF DERIVATIVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Slope of normal to the curve $y = x^{2} - x$ and x=2 is
A $- \frac{1}{3}$
B $- \frac{1}{7}$
C $- \frac{1}{9}$
D $- \frac{1}{11}$
The equation of normal to the curve $y = 6 - x^{2},$ where the normal is parallel to the line $x - 4 y + 3 = 0$ is
Ax-4y-6=0
Bx+4y-6=0
Cx-4y+6=0
Dx+4y+6=0
The equation of the normal to the curve $y = e^{- 2 | x |}$ at the point where the curve cuts the line $x = 1 / 2$ is
A $2 e (e x + 2 y) = e^{2} - 4$
B $2 e (e x - 2 y) = e^{2} - 4$
C $2 e (e y - 2 x) = e^{2} - 4$
Dnone of these

IIT JEE PREVIOUS YEAR-APPLICATION OF DERIVATIVES -MAXIMA AND MINIMA (ANALYTICAL & DESCRIPTIVE QUESTIONS )

Home
Ask Doubt
Profile