A helicopter flying along the path y=7+x32, A soldier standing at point (12,7) wants to hit the helicopter when it is closest from him, then minimum distance is equal to
13√73
√56
16√73
12
The correct Answer is:C
The helicopter is nearest to the soldier, if the tangent ot the path, y=x3/2+7,(x≥0) of helicopter at point (x,y) is perpendicular to the line joining (x,y) and the position of soldier (12,7).

∵ Slope of tangent at point (x,y) is
dydx=32x1/2=m1 (let) ...(i)
and slope of line joining (x,y)and(12,7) is
m2=y−7x−12 ...(ii)
Now, m1⋅m2=−1
⇒32x1/2(y−7x−(1/2))=−1 [ from Eqs. (i) and (ii)]
⇒ 32x1/2=x3/2x−12=−1 [∵y=x3/2=7]
⇒ 32x2=−x+12
⇒3x2+3x−x−1=0
⇒3x(x+1)−1(x+1)=0
⇒ x=13,−1
∵ x≥0
∴ x=13
and So, y=(13)3/2+7 [∵y=x3/2+7]
Thus, the nearest distance
=
⎷(12−13)2+(7−(13)3/2−7)2=√(16)2+(13)3
=√136+127=√3+4108=√7108=16√73
Topper's Solved these Questions
- APPLICATION OF DERIVATIVES Book:IIT JEE PREVIOUS YEARChapter:APPLICATION OF DERIVATIVES Exercise:EQUATIONS OF TANGENT AND NORMAL (OBJECTIVE QUESTIONS II )
Explore 2 Videos
- APPLICATION OF DERIVATIVES Book:IIT JEE PREVIOUS YEARChapter:APPLICATION OF DERIVATIVES Exercise:EQUATIONS OF TANGENT AND NORMAL ()
Explore 1 Video
- 3D GeometryBook:IIT JEE PREVIOUS YEARChapter:3D GeometryExercise:Equation of Plane Objective Question II (Integer Answer Type Question)
Explore 1 Video
- AREABook:IIT JEE PREVIOUS YEARChapter:AREAExercise:AREA USING INTEGRATION
Explore 55 Videos
Similar Questions
An Apache helicopter of enemy is flying along the curve given by y=x2+7. A soldier, placed at (3, 7), wants to shoot down the helicopter when it is nearest to him. Find the nearest distance.
View SolutionA helicopter is flying along the curve y=x2+2. A soldier is placed at the point (3, 2). Find the nearest distance between the solider and the helicopter.
View Solution
Knowledge Check
The minimum distance from the point (4, 2) to y2=8x is equal to
A√2B2√2C2D3√2The minimum distance of the point (1, 2, 3) from
x-axis isA1 unitB√6 unitsC√13 unitsD√14 unitsA helicopter is flying at 200m and flying at 25ms−1 at an angle 37∘ above the horizontal when a package is dropped from it.
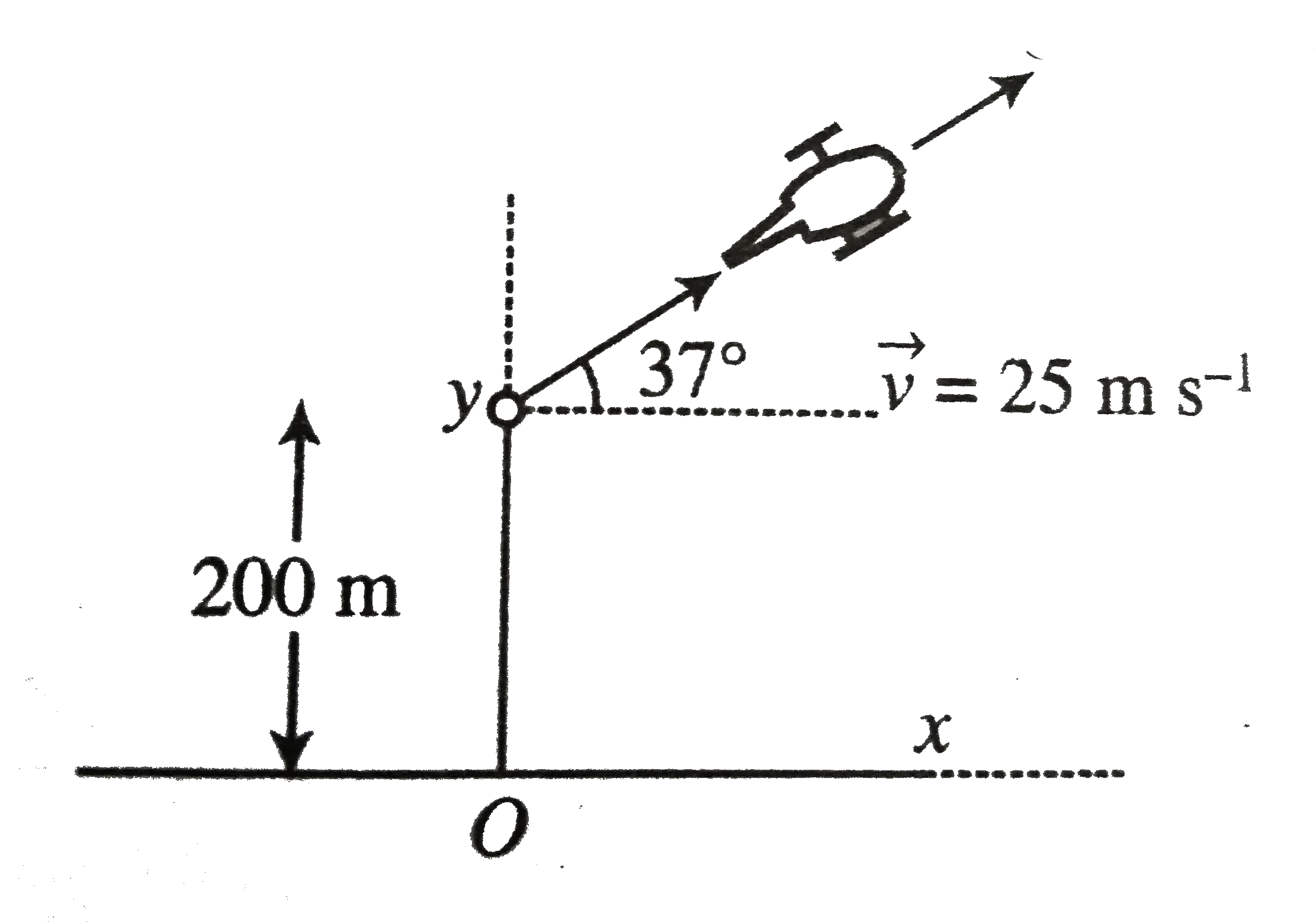
The distance of the point O where the package lands isA80 mB100 mC200 mD160 m
The point on the line 3x−2y=1 which is closest to the origin is
View SolutionQ is the image of point P(1, -2, 3) with respect to the plane x−y+z=7. The distance of Q from the origin is.
View SolutionA jet of enemy is along the curve y=x2+2 and a soldier is placed at (3,2).Find the minimum distance between the jet and soldier.
View SolutionThe point on the ellipse x2+2y2=6 closest to the line x+y=7 is
View SolutionA helicopter is flying at 200m and flying at 25ms−1 at an angle 37∘ above the horizontal when a package is dropped from it.
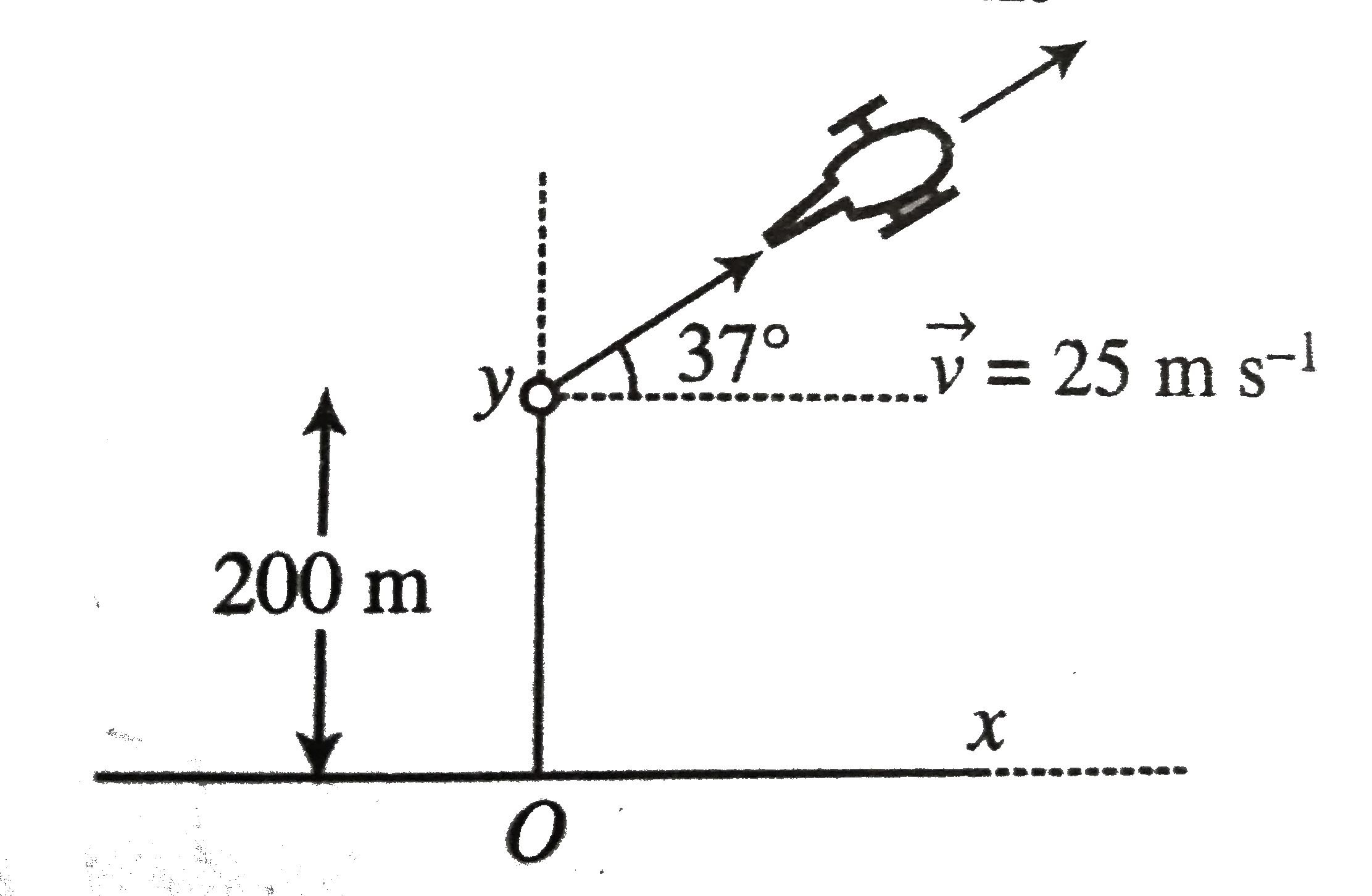
If the helicopter flies at constant velocity, find the x and y coordinates of the location of the helicopter when the package lands.
View Solution