Block A is hanging from a vertical spring and is at rest. Block B strikes the block A with velocity v and sticks to it. Then the value of v for which the spring just attains natural length is

√6mg2K
√3mg2K
√12mg2K
2√mg2K
The correct Answer is:A
Since the block is hanging in equilibrium hence extension of the spring is mg/K .
We can neglect finite forces like gravity at the time of collision and we can apply conaservation of linear momentum just before and just after the collision . Let v is the velocity of the block plus particle just after collision then
mu=(m+m)v⇒v=u2
Now the block and particle move upward and comes to rest when spring attains natural length . We can apply conservation of mechanical energy .
Loss in K.E + Loss in spring potential energy = gain in gravitational potentail energy .
1.2(2m)(u2)2+12K(mgK)2=(2m)g(mgK)
⇒ mu22+m2g2K=4m2g2K⇒u22=3mg2K
⇒ u=√6mg2K
Topper's Solved these Questions
- WORK, ENERGY AND POWER BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Objective Type Questions (B. Multiple Choice Questions)
46 Videos
- WORK, ENERGY AND POWER BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Objective Type Questions (JEE (Main) & Other State Boards for Engineering Entrance)
31 Videos
- WORK, ENERGY AND POWER BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Revision Exercise (Numerical Problems)
23 Videos
- WAVESBOOK - MODERN PUBLICATIONCHAPTER - WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
Similar Questions
A block A of mass 2m is hanging from a vertical massless spring of spring constant k and is in equilibrium. Another block B of mass m strikes the block A with velocity u and sticks to it as shown in the figure. The magnitude of the acceleration of the combined system of the blocks just after the collision is
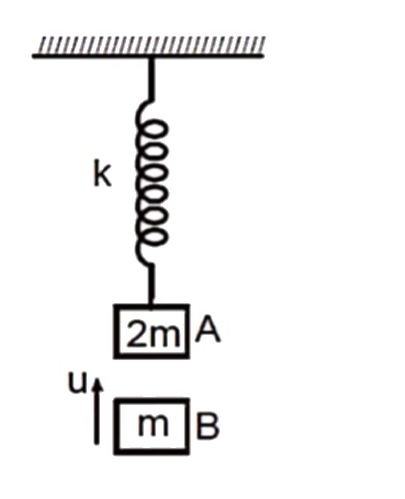
View SolutionThe ball strikes the block and sticks to it. Find the maximum compression of spring. (L: natural length of spring)

View Solution
Knowledge Check
Block A is hanging from vertical spring of spring constant K and is rest. Block B strikes block A with velocity v and sticks to it. Then the value of v for which the spring just attains natural length is
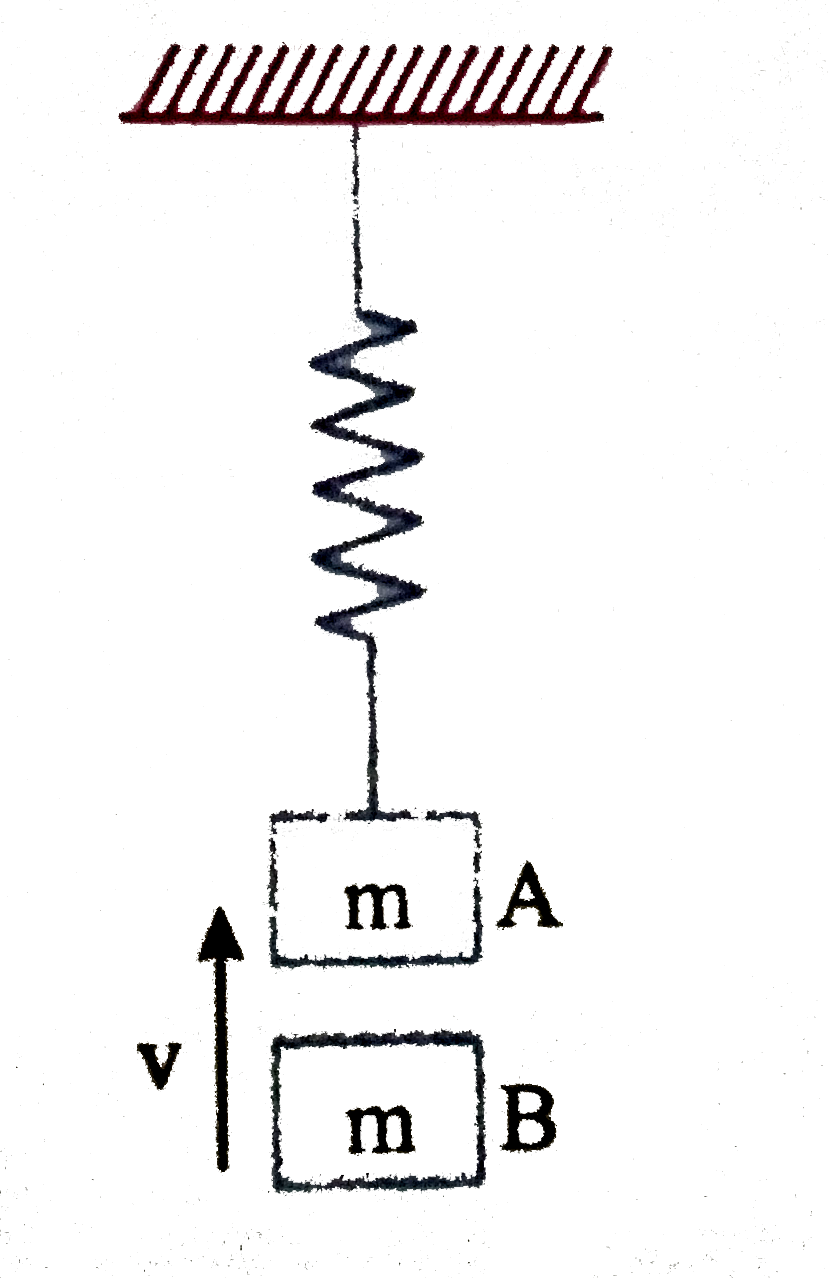 A√60mg2kB√6mg2kC√10mg2kD√mg2k
A√60mg2kB√6mg2kC√10mg2kD√mg2kTwo blocks A and B of masses in and 2m, respectively, are connected with the help of a spring having spring constant, k as shown in Fig. Initially, both the blocks arc moving with same velocity v on a smooth horizontal plane with the spring in its natural length. During their course of motion, block B makes an inelastic collision with block C of mass m which is initially at rest. The coefficient of restitution for the collision is 1/2. The maximum compression in the spring is
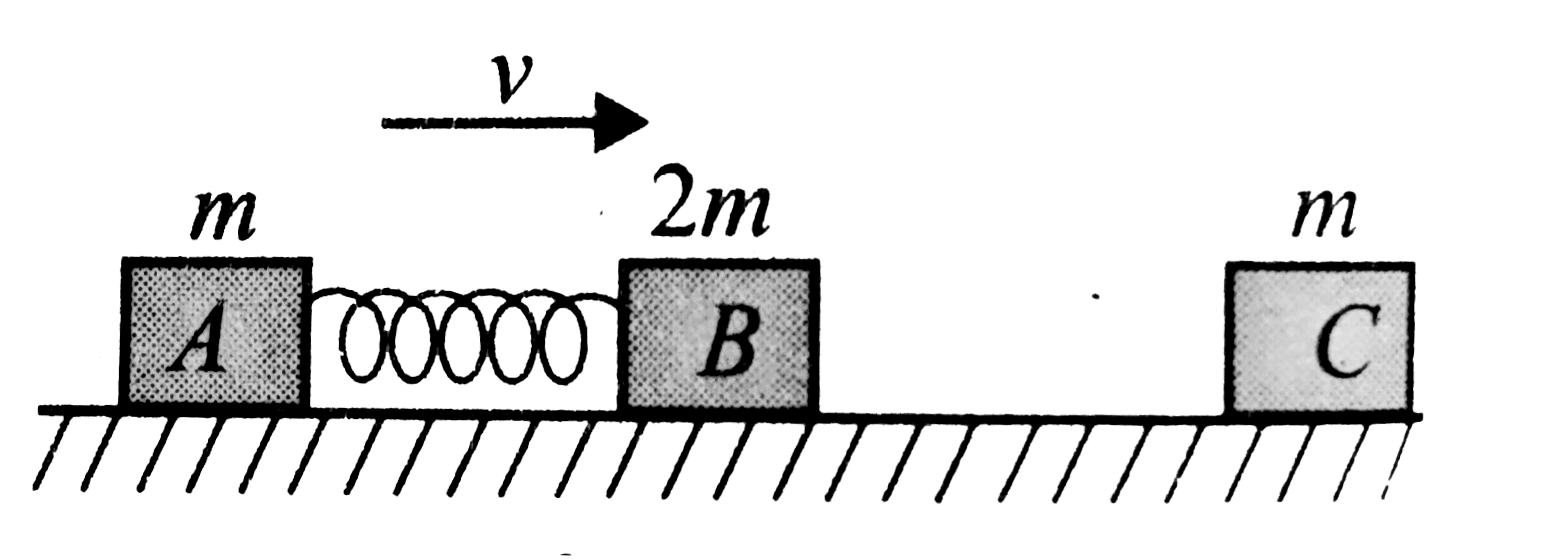 A√2mkBwill never be attainedC√m12kvD√m6kv
A√2mkBwill never be attainedC√m12kvD√m6kvTwo blocks A and B of the same mass are connected to a light spring and placed on a smooth horizontal surface B is given velocity v0 (as shown in the figure) when the spring is in natural length. In the subsequent motion.
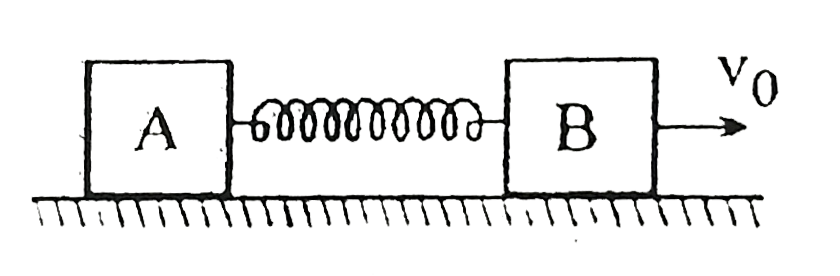 Athe maximum velocity of B will be v0Bas seen from ground, A can move towards right onlyCthe spring will have maximum extension when A and B both stopDthe spring will be at natural length again when B is at rest
Athe maximum velocity of B will be v0Bas seen from ground, A can move towards right onlyCthe spring will have maximum extension when A and B both stopDthe spring will be at natural length again when B is at rest
Two blocks A and B of masses m and 2m are connected by a massless spring of natural length L and spring constant k. The blocks are intially resting on a smooth horizontal floor with the spring at its natural length , as shown . A third identical block C of mass m moves on the floor with a speed v0 along the line joining A and B and collides elastically with A. FInd (a) the velocity of c.m. of system (blockA+B+spring) and (b) the minimum compression of spring.

View SolutionA block of mass 'm' is attached to a spring. Block is released from rest, when spring is in natural length. Block is along the pricipal axis of concave mirror and size of block is very small. When spring is in natural length then block is at a distance of 20 cm from the mirror, distance (in cm) in which the image formed by mirror oscillates is (mass of the block =5×10−2 kg, spring constant k=20 N//m)

View SolutionThe two blocks A and B of same mass connected to a spring and placed on a smooth surface. They are given velocities (as shown in the figure) when the spring is in its natural length :
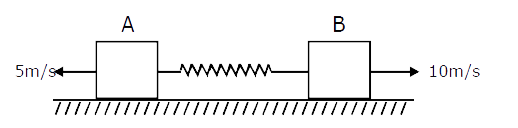
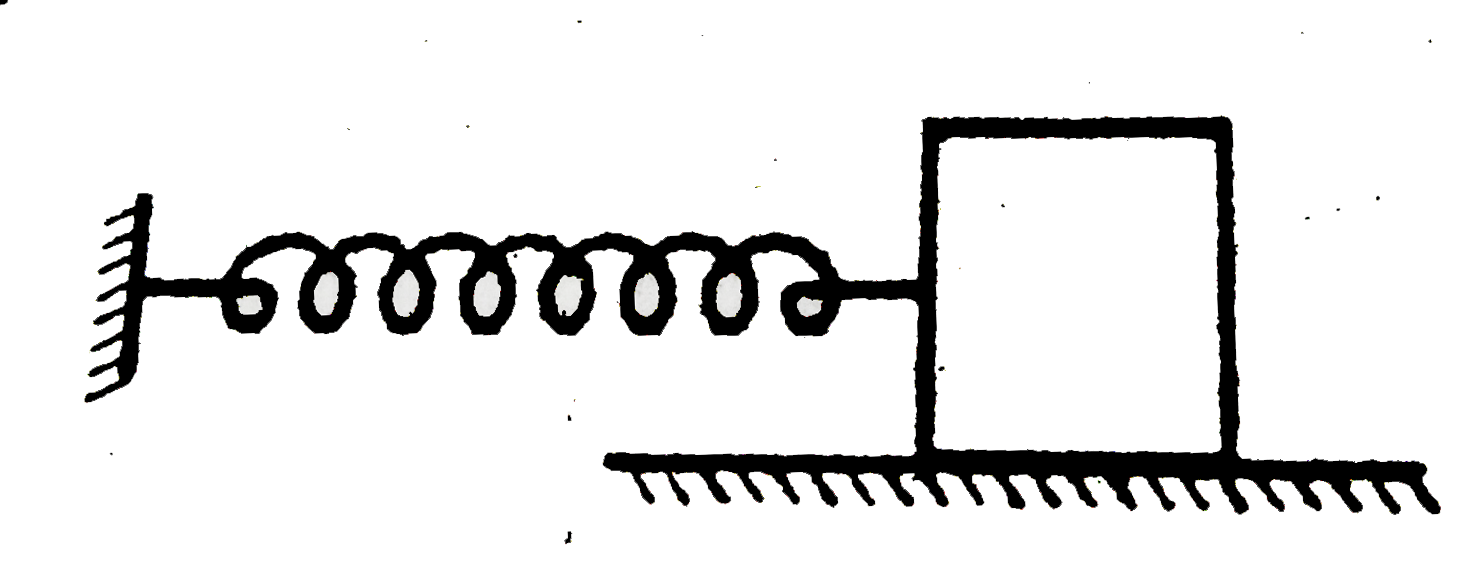
View SolutionA block is connected to a relaxed spring and kept on a smooth floor. The block is given a velocity towards the right. Just after this,
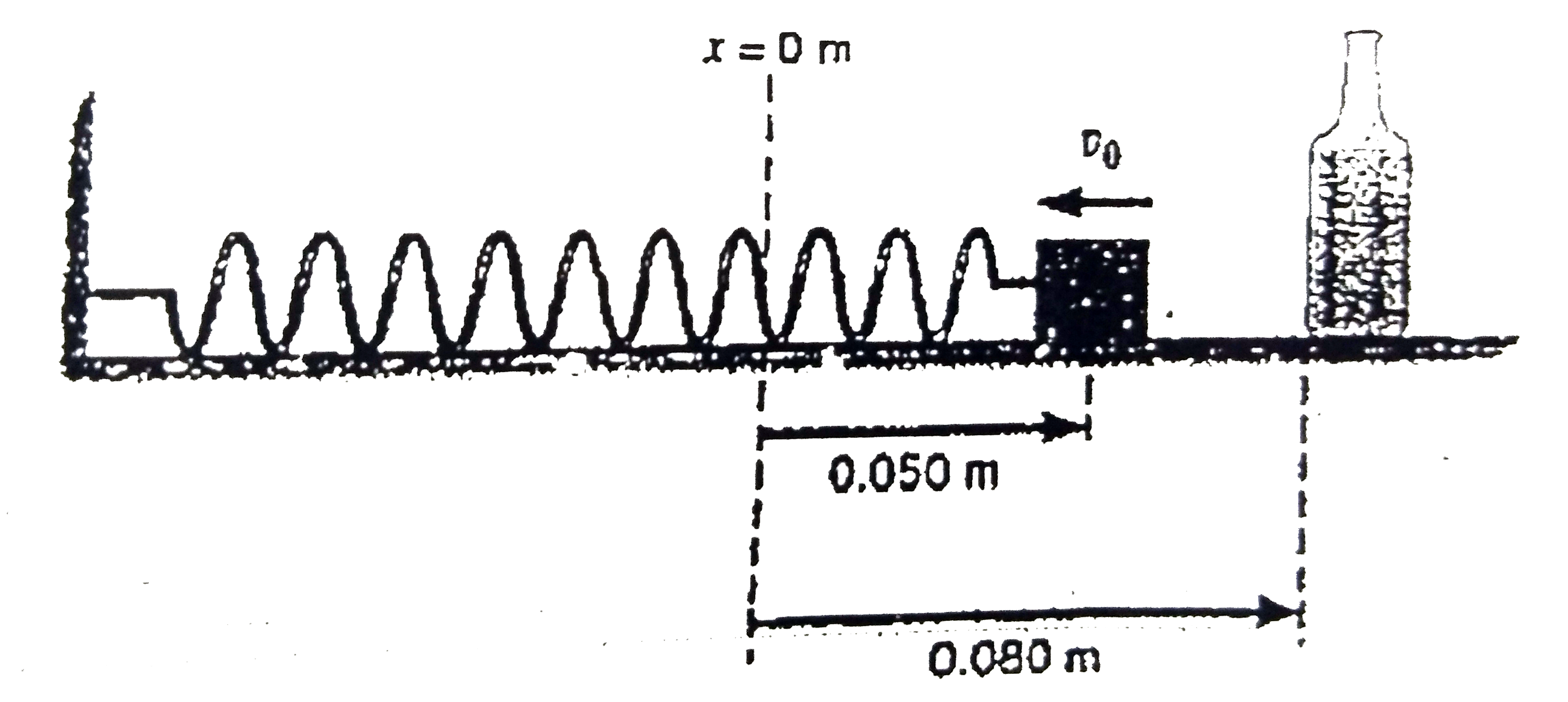
View SolutionThe elastic constant of the spring in figure is 25.00N/m and the mass of the block is 0.50 kg. If the block is to hit the bottle, what is minimum value of va. The spring has natural length when block is x=0m.
View Solution
