A block is connected to a relaxed spring and kept on a smooth floor. The block is given a velocity towards the right. Just after this,
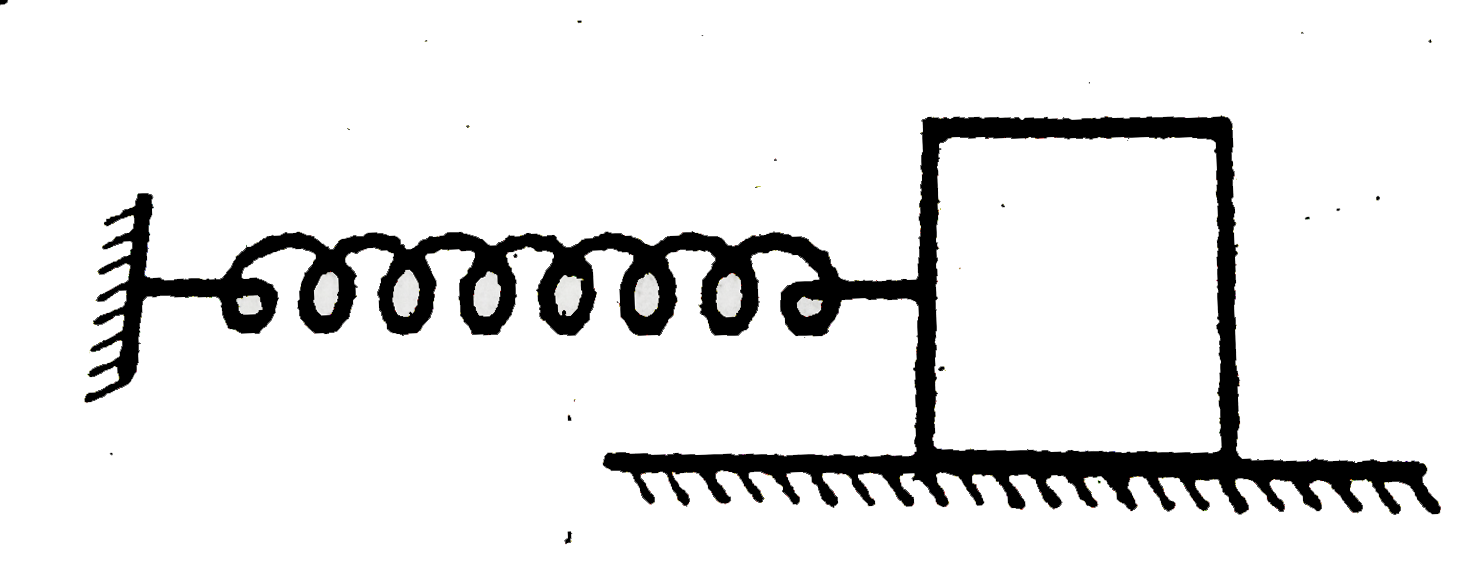
The speed of block starts decreasing but acceleration starts in increasing.
The speed of the block as well as its acceleration starts decreasing.
The speed of the block starts increasing but its acceleration starts decreasing.
The speed of the block as well as acceleration starts increasing.
The correct Answer is:A
a=kxm
12m(v2−u2)=−12kx2
Topper's Solved these Questions
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART (A)
Explore 32 Videos
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART (B)
Explore 3 Videos
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART- C
Explore 4 Videos
- SEMICONDUCTORSBook:BANSALChapter:SEMICONDUCTORSExercise:CBSE Question
Explore 32 Videos
Similar Questions
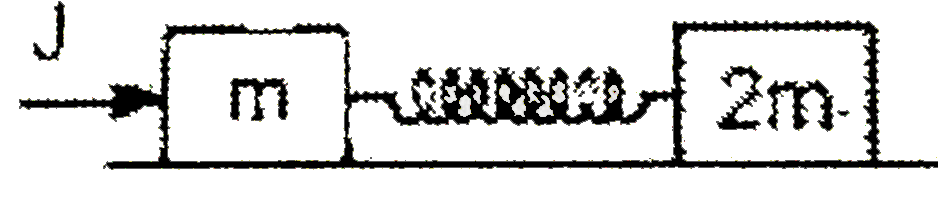
two blocks of masses m and 2m are connected by a relaxed spring with a force contant k. the block on the left is given a sharp irnpulse "J" towards the right , and the blocks begin to slide along the table ,(see fig 4E.3) find the maximum compression in the spring .
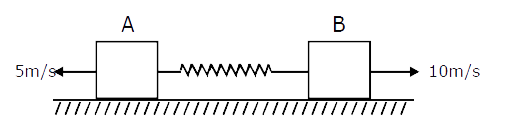
View SolutionThe two blocks A and B of same mass connected to a spring and placed on a smooth surface. They are given velocities (as shown in the figure) when the spring is in its natural length :
View Solution
Knowledge Check
Two blocks A and B of the same mass are connected to a light spring and placed on a smooth horizontal surface B is given velocity v0 (as shown in the figure) when the spring is in natural length. In the subsequent motion.
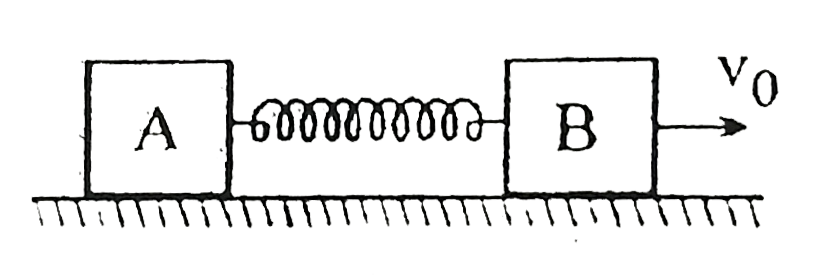 Athe maximum velocity of B will be v0Bas seen from ground, A can move towards right onlyCthe spring will have maximum extension when A and B both stopDthe spring will be at natural length again when B is at rest
Athe maximum velocity of B will be v0Bas seen from ground, A can move towards right onlyCthe spring will have maximum extension when A and B both stopDthe spring will be at natural length again when B is at restThree blocks of masses m , m and M are kept on a frictionless floor as shown in the figure .The leftmost block is given velocity v towards the right . All the collision between the blocks are perfectly inelastic . The loss in kinetic energy after all the collision is 5/6th of initial kinetic energy. The ratio of M/m will be
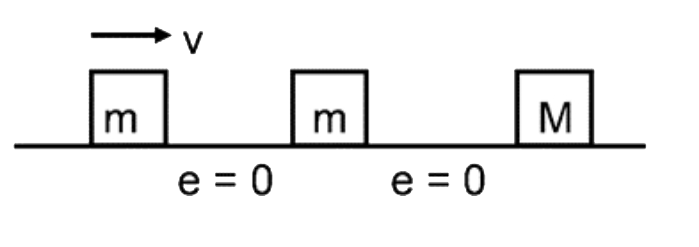 A14B18C2D4
A14B18C2D4A light spring of force constant 'K' is held between two blocks of masses 'm' and '2m'. The two blocks and the spring system rests on a smooth horizontal floor. Now th blocks are moved towards each other compressing the springs by 'x' and suddenly released. The relative velocity between the blocks when the spring attains its natural length will be
A(√3K2m)xB(√2K3m)xC(√K3m)xD(√K2m)x
The figure shows two blocks of mass m each, connected by an ideal unstretched spring and then placed on a frictionless floor. If the blocks are given velocities v0and2v0 as shown, then the maximum extension in the spring is
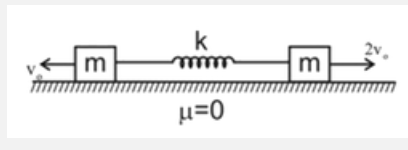
View SolutionA block of mass m=2kg is connected to a spring of force constant k=50n/m. Initially the block is at rest and the spring has natural length . A constant force f=60N, is applied horizontally towards right, the maximum speed of the block (in m/s will be (neglect frication).

View Solution
A block A of mass m is placed on a smooth horizontal platform P and between two elastic massless springs S1 and S2 fixed horizontally to two fixed vertical walls. The elastic constants of the two springs are equal to k and the equilibrium distance between the two springs both in relaxed states is d. The block is given a velocity v0 initially towards one of the springs and it then oscillated between the springs. The time period T of oscillations and the minimum separation dm of the spring will be
View Solution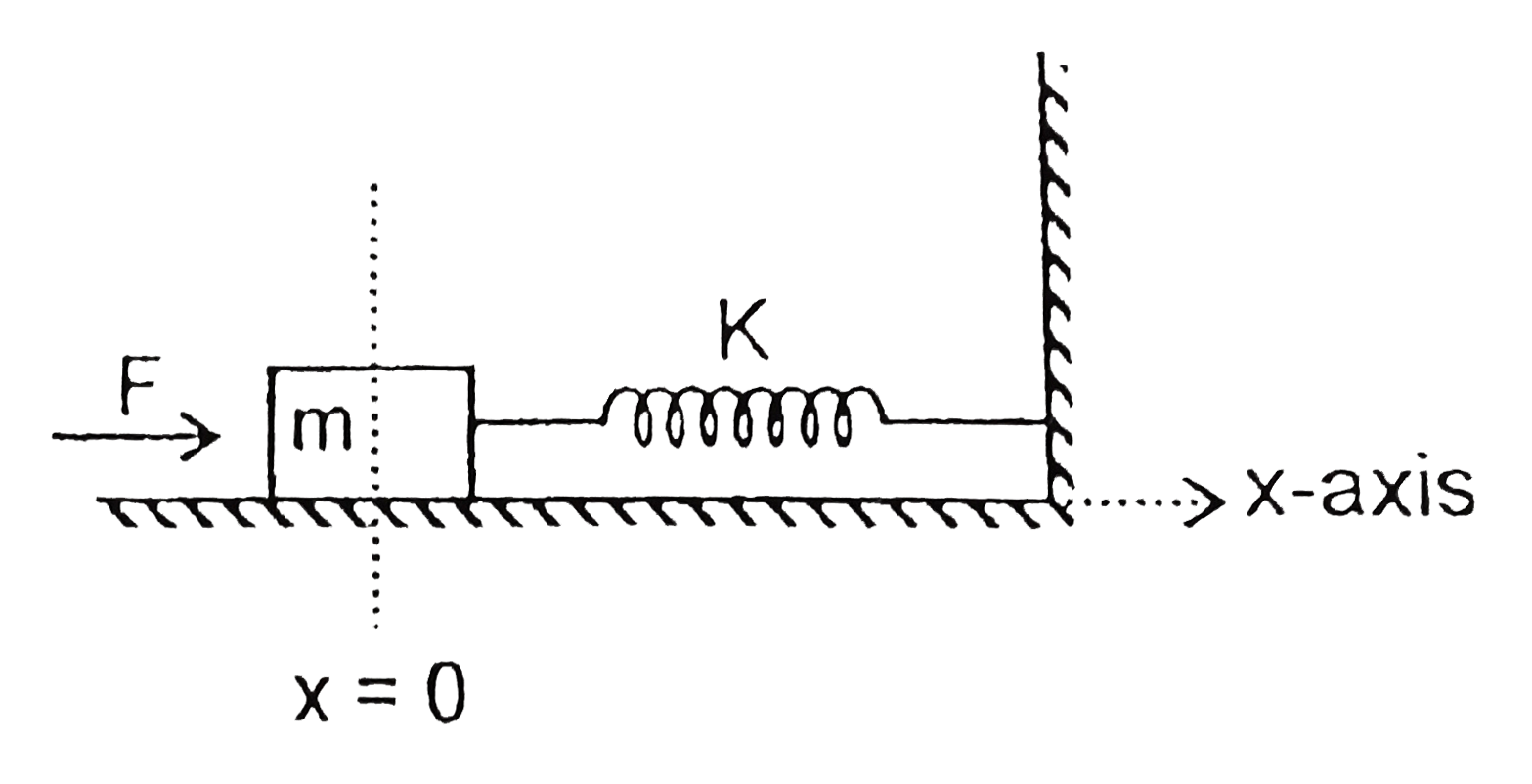
A block of mass m connected to a spring of stiffness k is placed on horizontal smooth surface. When block is at x=0, spring is in natural length. The block is also subjected to a force F=k|x|∘ then
View Solution
A block of mass m is attached to two unstretched springs of spring constant k, each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will be
View Solution

