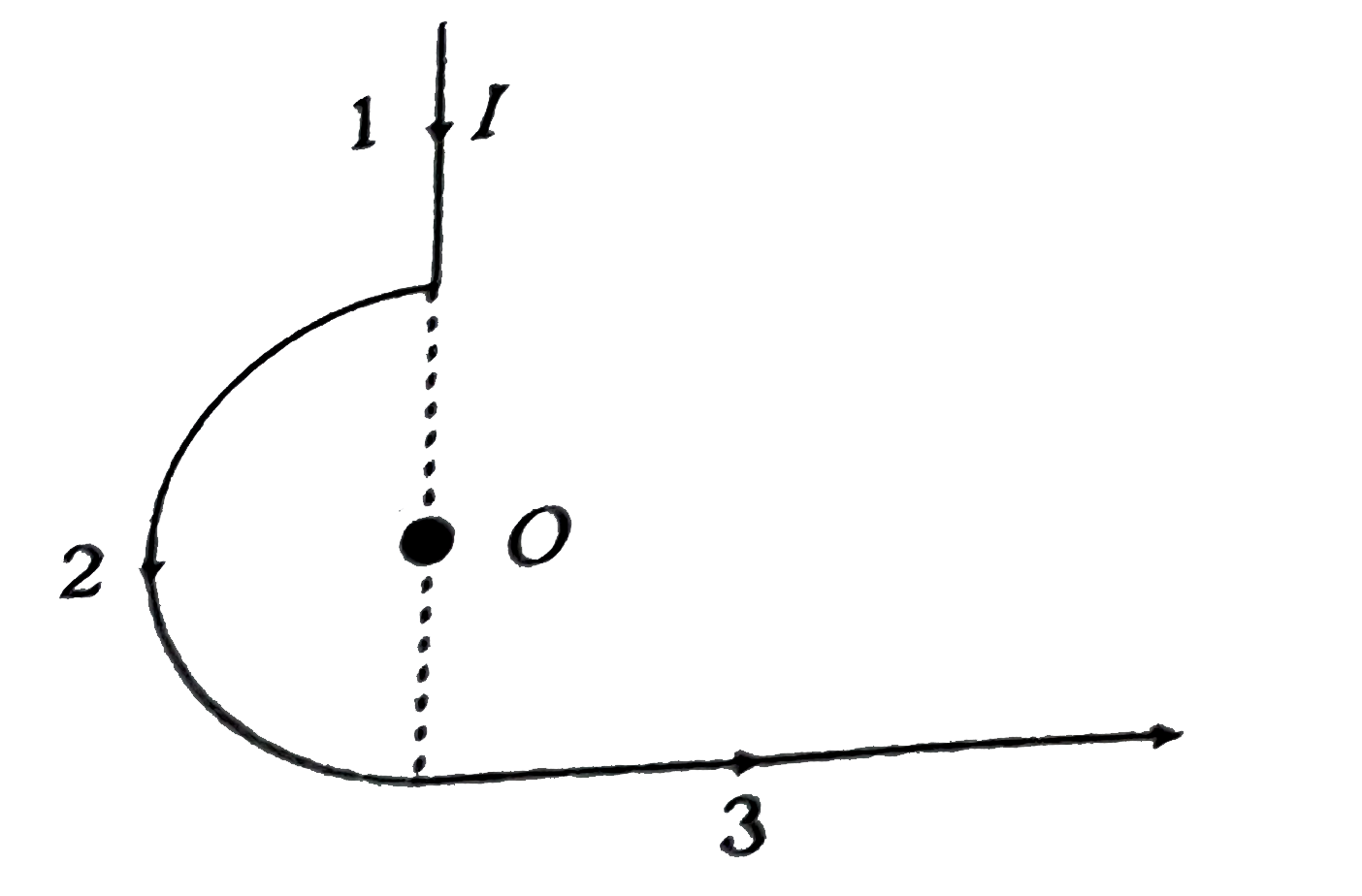
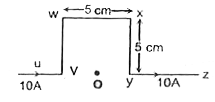
Find the magnetic field at the origin due to the combination of two semi infinite wires and a semicircular wire as shown.

Video Solution
Text Solution
The magnetic field at the centre O due to the two straight sent infinite parts of conductor is
−→B1=μ04π.iaˆk+μ04π.iaˆk=μ04π.2iaˆk …(1)
The magnetic field due to the semicircular part is
−→B2=μ04π.πia(−ˆj) ....(2)
∴ The net magnetic field at the centre O is
→B=vev(B1)+−→B2=μ04π.ia(2ˆk−πˆj) ......(3)
|
Topper's Solved these Questions
- MAGNETICBook:FIITJEEChapter:MAGNETICExercise:Assignment Problems (Subjective) (Level-I)
Explore 15 Videos
- MAGNETICBook:FIITJEEChapter:MAGNETICExercise:Assignment Problems (Subjective) (Level - II & III)
Explore 15 Videos
- MAGNETICBook:FIITJEEChapter:MAGNETICExercise:Matrix match Type
Explore 8 Videos
- LAWS OF MOTIONBook:FIITJEEChapter:LAWS OF MOTIONExercise:COMPREHENSION-III
Explore 2 Videos
- MAGNETISMBook:FIITJEEChapter:MAGNETISMExercise:Example
Explore 12 Videos
Similar Questions
Knowledge Check
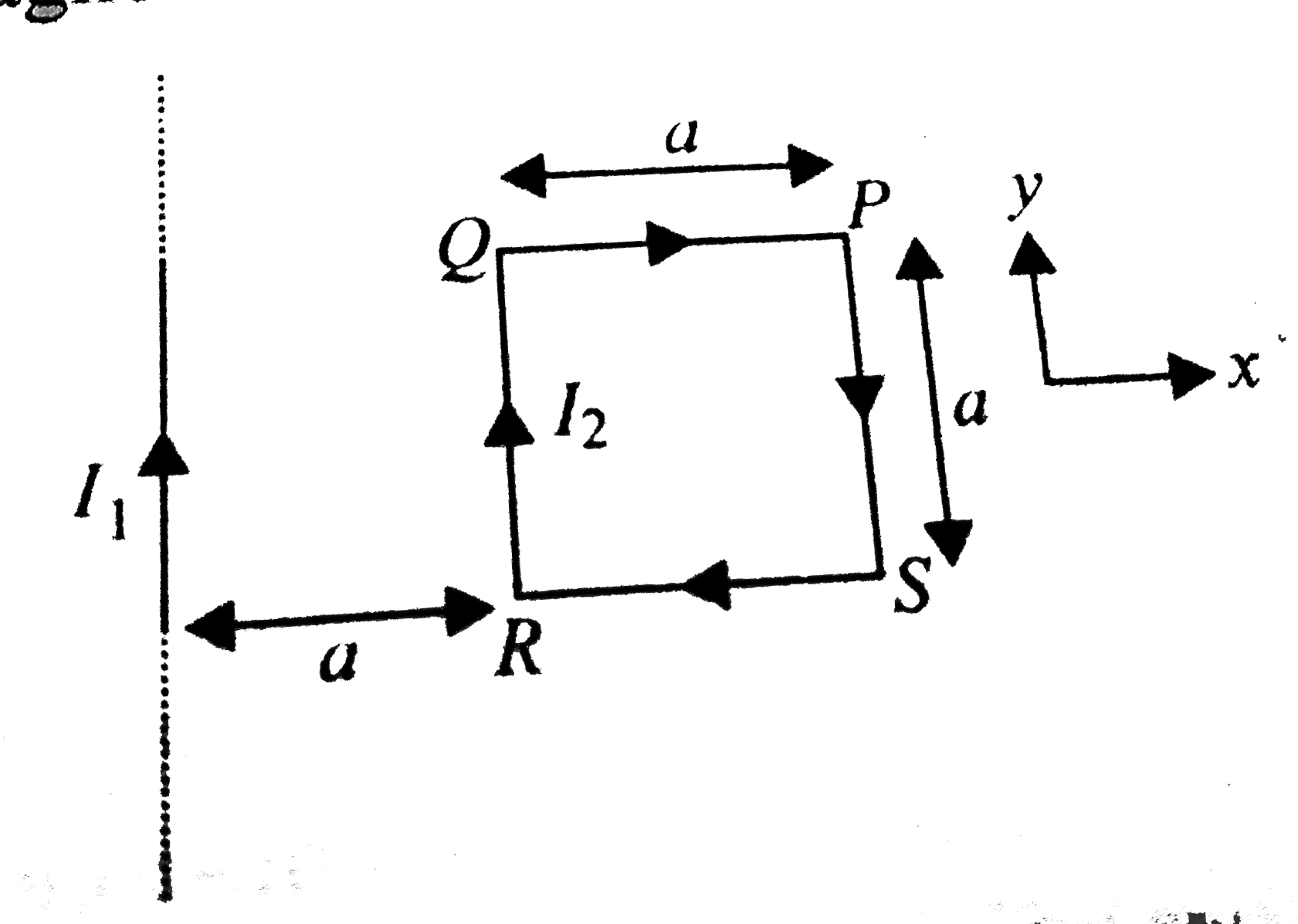
The magnetic field at the origin due to the current flowing in the wire is
 A−μ0I8πa(ˆi+ˆk)Bμ0I2πa(ˆi+ˆk)Cμ0I8πa(−ˆi+ˆk)D−μ0I4πa√2(ˆi−ˆk)
A−μ0I8πa(ˆi+ˆk)Bμ0I2πa(ˆi+ˆk)Cμ0I8πa(−ˆi+ˆk)D−μ0I4πa√2(ˆi−ˆk)The magnetic field at O due to current in the infinite wire forming a loop as a shown in Fig.
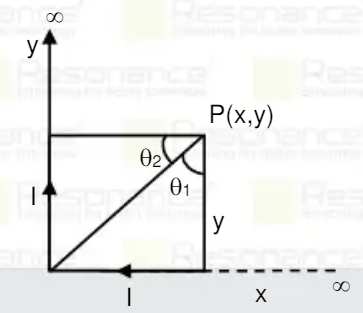
 Aμ0I2πd(cosϕ1+cosϕ2)Bμ04π2Id(tanθ1+tanθ2)Cμ04πId(sinϕ1+sinϕ2)Dμ04πId(cosθ1+cosθ2)
Aμ0I2πd(cosϕ1+cosϕ2)Bμ04π2Id(tanθ1+tanθ2)Cμ04πId(sinϕ1+sinϕ2)Dμ04πId(cosθ1+cosθ2)Magnetic field produced at the point O due to current flowing in an infinite wire shaped as shown in the figure is
 Aμ0I4πRBμ0I4R−μ0I4πRCμ0I4R−μ0I2πRDμ0I4R+μ0I4πR
Aμ0I4πRBμ0I4R−μ0I4πRCμ0I4R−μ0I2πRDμ0I4R+μ0I4πR
Find magnetic induction at P due to wire:
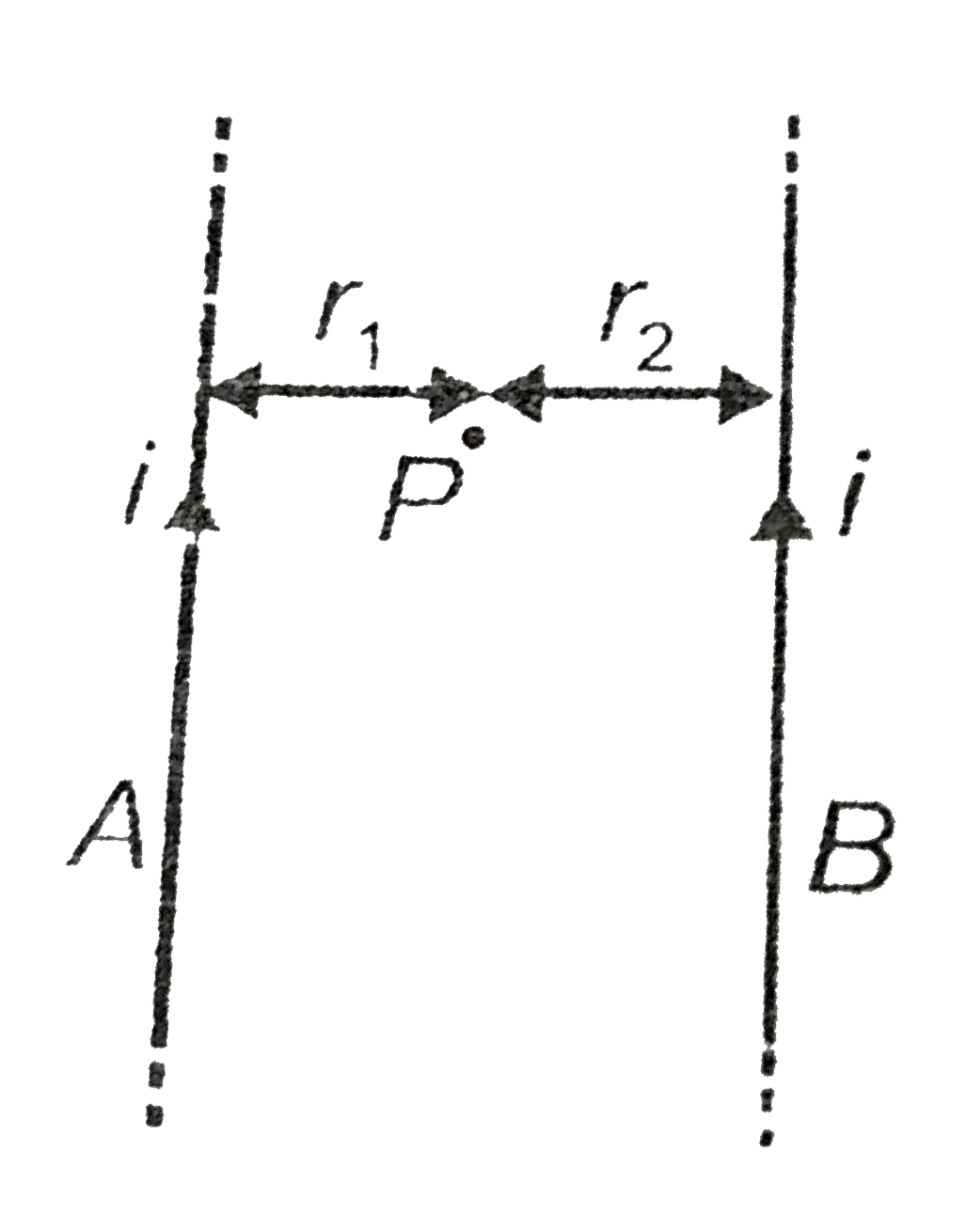
View SolutionFind the direction of magnetic field at a point P due to two infinite current carrying wires shown in the figure. Given r1>r2
View SolutionThe resulting magnetic field at the point O due to the current carrying wire shown in the figure-
View SolutionWhat will be the resulatant field at the origin due to the four indinite length wires if each wire produces magnetic field B at origin ?
View SolutionThe resulting magnetic field at the point O due to the current carrying wire shown in the figure:
View Solution