Two similar current loops are placed with their planes mutually perpendicular and centres of both loop lie on the origin. Find the ratio of resultant magnetic field at common centre to the individual magnetic field at common centre.
To solve the problem of finding the ratio of the resultant magnetic field at the common center of two mutually perpendicular current loops to the individual magnetic field at that center, we can follow these steps:
Step 1: Understand the Configuration
We have two similar current loops placed at the origin with their planes mutually perpendicular. Let’s denote:
- Loop 1 is in the XY-plane (current flowing in a circular manner).
- Loop 2 is in the YZ-plane (current flowing in a circular manner).
Step 2: Determine the Magnetic Field Due to Each Loop
The magnetic field at the center of a single circular loop carrying current I and having radius R is given by the formula:
B=μ04π⋅2πIR
This simplifies to:
B=μ0I2R
Since both loops are similar (same radius R and same current I), the magnetic fields at the center due to each loop will be equal:
B1=B2=B=μ0I2R
Step 3: Determine the Direction of the Magnetic Fields
Using the right-hand rule:
- For Loop 1 (XY-plane), the magnetic field B1 points in the negative Z-direction (let's denote it as −^k).
- For Loop 2 (YZ-plane), the magnetic field B2 points in the negative X-direction (let's denote it as −^i).
Step 4: Calculate the Resultant Magnetic Field
Since B1 and B2 are perpendicular to each other, the resultant magnetic field BRES can be calculated using the Pythagorean theorem:
BRES=√B21+B22
Substituting the values:
BRES=√B2+B2=√2B2=B√2
Step 5: Find the Ratio of Resultant Magnetic Field to Individual Magnetic Field
Now, we need to find the ratio of the resultant magnetic field to the individual magnetic field:
Ratio=BRESB=B√2B=√2
Final Answer
Thus, the ratio of the resultant magnetic field at the common center to the individual magnetic field at the common center is:
Ratio=√2:1
We have two similar current loops placed at the origin with their planes mutually perpendicular. Let’s denote:
- Loop 1 is in the XY-plane (current flowing in a circular manner).
- Loop 2 is in the YZ-plane (current flowing in a circular manner).
The magnetic field at the center of a single circular loop carrying current I and having radius R is given by the formula:
B=μ04π⋅2πIR
This simplifies to:
B=μ0I2R
Since both loops are similar (same radius R and same current I), the magnetic fields at the center due to each loop will be equal:
B1=B2=B=μ0I2R
Using the right-hand rule:
- For Loop 1 (XY-plane), the magnetic field B1 points in the negative Z-direction (let's denote it as −^k).
- For Loop 2 (YZ-plane), the magnetic field B2 points in the negative X-direction (let's denote it as −^i).
Since B1 and B2 are perpendicular to each other, the resultant magnetic field BRES can be calculated using the Pythagorean theorem:
BRES=√B21+B22
Substituting the values:
BRES=√B2+B2=√2B2=B√2
Now, we need to find the ratio of the resultant magnetic field to the individual magnetic field:
Ratio=BRESB=B√2B=√2
Thus, the ratio of the resultant magnetic field at the common center to the individual magnetic field at the common center is:
Ratio=√2:1
Topper's Solved these Questions
- MAGNETICBook:FIITJEEChapter:MAGNETICExercise:Assignment Problems (Subjective) (Level-I)
Explore 15 Videos
- MAGNETICBook:FIITJEEChapter:MAGNETICExercise:Assignment Problems (Subjective) (Level - II & III)
Explore 15 Videos
- MAGNETICBook:FIITJEEChapter:MAGNETICExercise:Matrix match Type
Explore 8 Videos
- LAWS OF MOTIONBook:FIITJEEChapter:LAWS OF MOTIONExercise:COMPREHENSION-III
Explore 2 Videos
- MAGNETISMBook:FIITJEEChapter:MAGNETISMExercise:Example
Explore 12 Videos
Similar Questions
Knowledge Check
Two current loops (similar) are placed with their planes one along x-axis and the other along y-axis. Then the ratio of resultant magnetic field at a common point on the axis to the individual magnetic field at the same point is
A√2:1B1:√2C3:2D√3:√2In the given loop the magnetic field at the centre O is
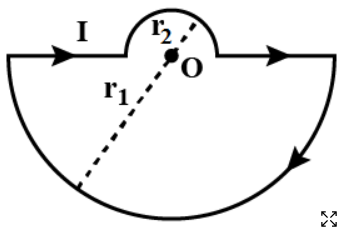 AμI4(r1+r2r1r2) out of the pageBμ0I4(r1+r2r1r2) into the pageCμ0I4(r1−r2r1r2) out of the pageDμ0I4(r1−r2r1r2) into the page
AμI4(r1+r2r1r2) out of the pageBμ0I4(r1+r2r1r2) into the pageCμ0I4(r1−r2r1r2) out of the pageDμ0I4(r1−r2r1r2) into the pageTwo similar coils are kept mutually perpendicular such that their centres coincide. At the centre, find the ratio of the magnetic field due to one coil and the resultant magnetic field by both coils, if the same current is flown
A1:√2B1:2C2:1D√3:1
Find the magnetic field at the centre of the circular loop shown in figure.

View SolutionFind the magnetic field at the centre O of the loop shown in the figure
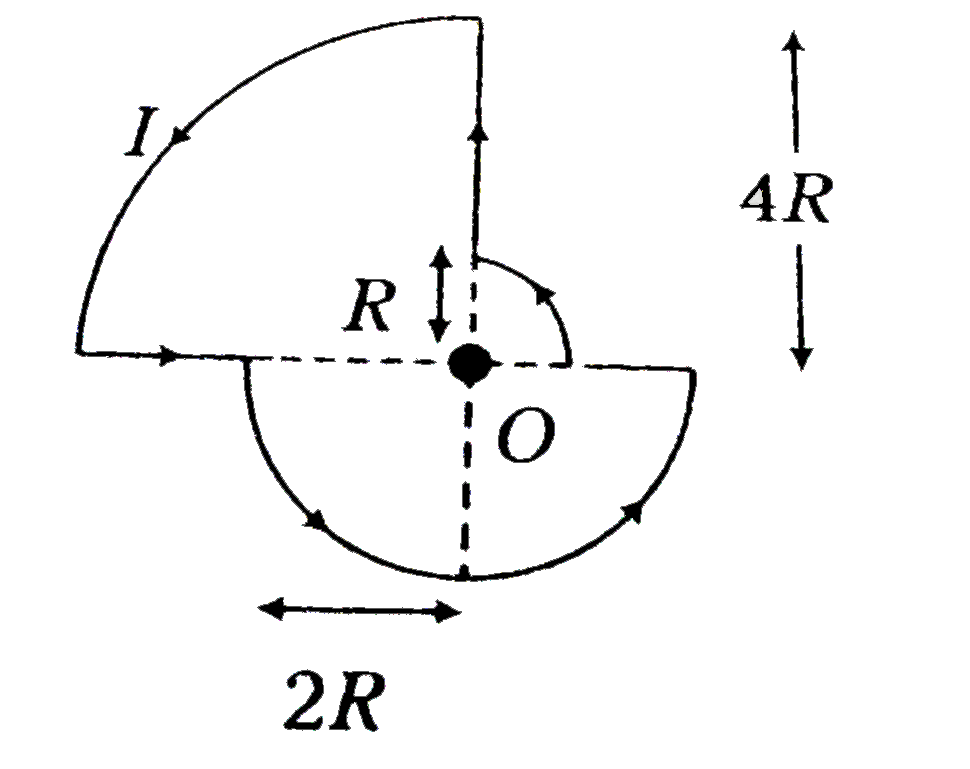
View SolutionFind the magnetic field at the centre of the circular loop shown in figure.

View SolutionA current I is flowing through the loop , as shown in the figure . The magnetic field at centre O is
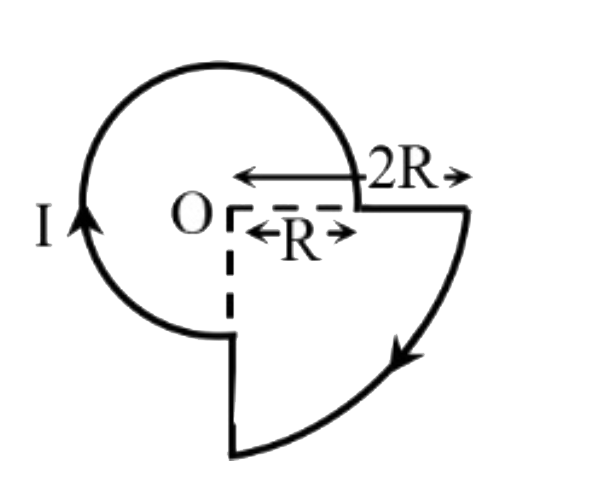
View SolutionA current loop placed in a magnetic field behaves like a
View Solution



