Question

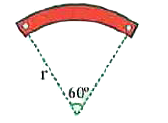
A thin bar magnet of length L is bent in the middle to from an angle of ${60}^{\circ }$ . The new length of the magnet is .

Options

A. L
B. 2L
C. `(L)/(2)`
D. `(L)/(sqrt(2))`

Answer

D

Explanation

To find the new length of a thin bar magnet that has been bent in the middle to form an angle of $${60}^{\circ }$$, we can follow these steps:

Step 1: Understand the initial length of the magnet
The initial length of the bar magnet is given as \(L\). When the magnet is bent in the middle, each half of the magnet will have a length of \( \frac{L}{2} \).

Step 2: Identify the angles involved
When the magnet is bent at an angle of \(60^\circ\), we can visualize the two halves of the magnet forming a triangle with the angle at the bend being \(60^\circ\).

Step 3: Determine the projection of each half
To find the effective length of the bent magnet, we need to consider the horizontal projections of each half of the magnet. The projection of each half can be calculated using the cosine of the angle formed by the bend.

Step 4: Calculate the projection
The projection of each half of the magnet is given by:
\( \text{Projection} = \frac{L}{2} \cos(30^\circ) \)
Since the angle \( \theta \) at each end of the bent magnet is \(30^\circ\) (because \(2\theta + 60^\circ = 180^\circ\) leads to \(2\theta = 120^\circ\) and thus \( \theta = 60^\circ\)), we have:
\( \cos(30^\circ) = \frac{\sqrt{3}}{2} \)

Step 5: Calculate the total effective length
The total effective length of the bent magnet is the sum of the projections of both halves:
\( \text{New Length} = 2 \left( \frac{L}{2} \cos(30^\circ) \right) = L \cos(30^\circ) \)

Step 6: Substitute the value of cosine
Now substituting the value of \( \cos(30^\circ) \):
\( \text{New Length} = L \cdot \frac{\sqrt{3}}{2} \)

Final Answer
Thus, the new length of the magnet after bending it at \(60^\circ\) is:
\( \text{New Length} = \frac{L \sqrt{3}}{2} \)

---