A bar magnet of magnetic moment 'M' is bent in the form of an arc which makes angle 600. The percentage change in the magnetic moment is
9%increase
9%Decrease
4.5%Decrease
4.5% Increase
The correct Answer is:C
To solve the problem of finding the percentage change in the magnetic moment of a bar magnet bent into an arc of 60 degrees, we can follow these steps:
Step 1: Understand the initial conditions
The initial magnetic moment M of the bar magnet is given. We denote the pole strength as m and the effective length of the magnet as l. The magnetic moment can be expressed as:
M=m⋅l
Step 2: Determine the new effective length after bending
When the bar magnet is bent into an arc that subtends an angle of 60∘, we need to find the new effective length of the magnet. The arc length L corresponding to this angle can be calculated using the formula:
L=θ360∘×2πr
where θ=60∘.
Step 3: Calculate the radius of the arc
From the above formula, we can rearrange to find the radius r:
L=60360×2πr=16×2πr=πr3
Thus, we have:
r=3Lπ
Step 4: Find the new magnetic moment
After bending, the new effective length l′ is the chord length corresponding to the arc. In an equilateral triangle formed by the two ends of the arc and the center, the effective length can be calculated as:
l′=2rsin(60∘2)=2rsin(30∘)=2r⋅12=r
Substituting r:
l′=3Lπ
The new magnetic moment M′ is given by:
M′=m⋅l′=m⋅3Lπ
Step 5: Calculate the percentage change in magnetic moment
Now we can find the percentage change in magnetic moment:
Percentage Change=M′−MM×100
Substituting M′ and M:
Percentage Change=(m⋅3Lπ)−(m⋅l)m⋅l×100
This simplifies to:
Percentage Change=3Lπ−ll×100
Step 6: Substitute L with l
Since L=l (the original length of the magnet), we can substitute:
Percentage Change=3lπ−ll×100=(3π−1)×100
Step 7: Calculate the numerical value
Using π≈3.14:
Percentage Change=(33.14−1)×100≈(0.955−1)×100≈−4.45%
Thus, the percentage change in the magnetic moment is approximately −4.46%.
Final Answer
The percentage change in the magnetic moment is approximately 4.46% decrease.
---
The initial magnetic moment M of the bar magnet is given. We denote the pole strength as m and the effective length of the magnet as l. The magnetic moment can be expressed as:
M=m⋅l
When the bar magnet is bent into an arc that subtends an angle of 60∘, we need to find the new effective length of the magnet. The arc length L corresponding to this angle can be calculated using the formula:
L=θ360∘×2πr
where θ=60∘.
From the above formula, we can rearrange to find the radius r:
L=60360×2πr=16×2πr=πr3
Thus, we have:
r=3Lπ
After bending, the new effective length l′ is the chord length corresponding to the arc. In an equilateral triangle formed by the two ends of the arc and the center, the effective length can be calculated as:
l′=2rsin(60∘2)=2rsin(30∘)=2r⋅12=r
Substituting r:
l′=3Lπ
The new magnetic moment M′ is given by:
M′=m⋅l′=m⋅3Lπ
Now we can find the percentage change in magnetic moment:
Percentage Change=M′−MM×100
Substituting M′ and M:
Percentage Change=(m⋅3Lπ)−(m⋅l)m⋅l×100
This simplifies to:
Percentage Change=3Lπ−ll×100
Since L=l (the original length of the magnet), we can substitute:
Percentage Change=3lπ−ll×100=(3π−1)×100
Using π≈3.14:
Percentage Change=(33.14−1)×100≈(0.955−1)×100≈−4.45%
The percentage change in the magnetic moment is approximately 4.46% decrease.
Topper's Solved these Questions
- MAGNETISMBOOK - NARAYNACHAPTER - MAGNETISMEXERCISE - LEVEL-III(C.W)
30 Videos
- MAGNETISMBOOK - NARAYNACHAPTER - MAGNETISMEXERCISE - NCERT Based Questions
17 Videos
- MAGNETISMBOOK - NARAYNACHAPTER - MAGNETISMEXERCISE - LEVEL-I(C.W)
52 Videos
- EXPERIMENTAL PHYSICSBOOK - NARAYNACHAPTER - EXPERIMENTAL PHYSICSEXERCISE - Comprehension type
6 Videos
- MAGNETISM AND MATTERBOOK - NARAYNACHAPTER - MAGNETISM AND MATTEREXERCISE - EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)
17 Videos
Similar Questions
A bar magnet of magnetic moment "M" is bent in the 'U' shape such that all the parts are of equal lengths.Then the new magnetic moment
View SolutionA magnetized wire of magnetic moment M is bent into an are of a circle that subtends an angle of 30° at the centre. The equivalent magnetic moment is found to be Q times M. The numerical value of M should be _____
View Solution
Knowledge Check
A bar magnet of moment M is bent into arc, its moment
AdecreasesBincreasesCdoes not changeDmay changeA bar magnet of magnetic moment M is bent in the form of quadrant of circular arc . The new magnetic moment is
A2MπB2√2MπC√2MπDMA bar magnet of length and magnetic dipole moment 'M' is bent in the form of an arc as shown in figure. The new magnetic dipole moment will be
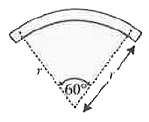 A2πMBM2CMD3πM
A2πMBM2CMD3πM
A bar magnet of l length and magnetic dipole moment M is bent in the form of an arc as shown in the figure. The new magnetic dipole moment will be

View SolutionA bar magnet of lenth l and magnetic dipole moment 'M' is bent in the form of an arc as shown in figure. The new magnetic dipole moment will be

View SolutionA magnetised wire of moment M is bent into an arc of a circle subtending an angle of 60^(@) at the centre. The new magnetic moment is

View SolutionA bar magnet of length l and magnet dipole moment M is bent in the form of an arc. The new magnetic dipole moment is
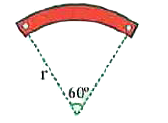
View SolutionA bar magnet of magnetic moment M is bent in
 shape with equal arm lengths.The new magnet moment is
shape with equal arm lengths.The new magnet moment is
View Solution