The two ends of a uniform rod of thermal conductivity k are maintained at different but constant temperatures. The temperature gradientat any point on the rod is dθdl(equal to the difference in temperature per unit length). The heat flow per unit time per unit cross-section of the rod is l then which of the following statements is/are correct:
dθdl is the same for all points on the rod.
l will decrease as we move from higher to lower temperature.
l=k.dθdl
All the above options are incorrect.
The correct Answer is:A, C, D
Step by step video, text & image solution for The two ends of a uniform rod of thermal conductivity k are maintained at different but constant temperatures. The temperature gradientat any point on the rod is (d theta)/(dl)(equal to the difference in temperature per unit length). The heat flow per unit time per unit cross-section of the rod is l then which of the following statements is/are correct: by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- HEAT AND TEMPERATUREBook:FIITJEEChapter:HEAT AND TEMPERATUREExercise:COMPREHENSIONS-I
Explore 3 Videos
- HEAT AND TEMPERATUREBook:FIITJEEChapter:HEAT AND TEMPERATUREExercise:COMPREHENSIONS-II
Explore 2 Videos
- HEAT AND TEMPERATUREBook:FIITJEEChapter:HEAT AND TEMPERATUREExercise:ASSIGNMENT PROBLEMS (OBJECTIVE) (LEVEL-I) (ASSERTION AND REASON)
Explore 2 Videos
- GRAVITATIONBook:FIITJEEChapter:GRAVITATIONExercise:Numerical based Question
Explore 2 Videos
- KINEMATICSBook:FIITJEEChapter:KINEMATICSExercise:NUMERICAL BASED QUESTIONS DECIMAL TYPE
Explore 5 Videos
Similar Questions
One end of the rod of length l, thermal conductivity K and area of cross-section A is maintained at a constant temperature of 100∘C. At the other end large quantity of ice is kept at 0∘C . Due to temperature difference, heat flows from left end to right end of the rod. Due to this heat ice will start melting. Neglecting the radiation losses find the expression of rate of melting of ice.
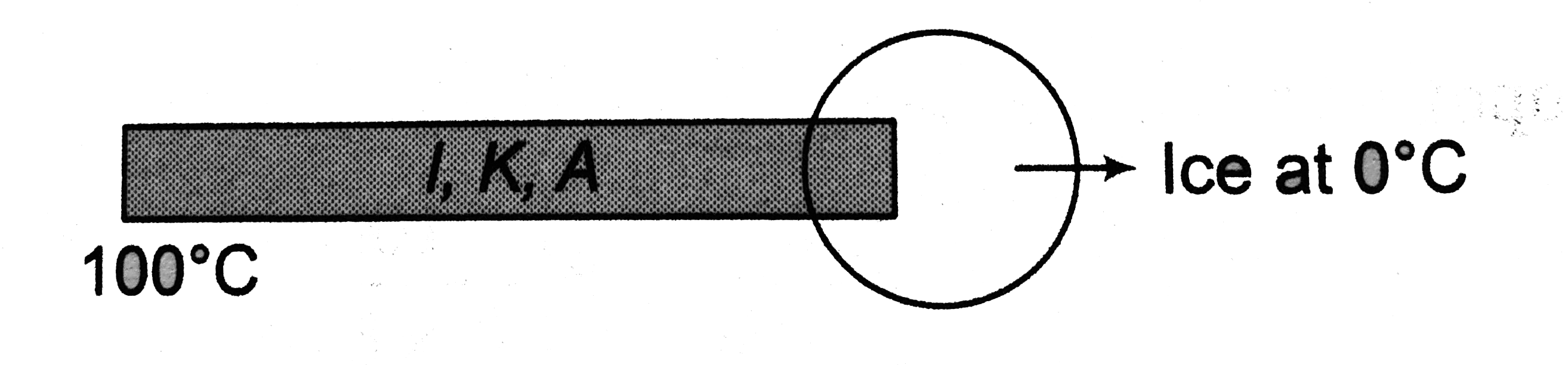 .
.
View SolutionWhen two ends of a rod wrapped with cotton are maintained at different temperatures and after some time every point of the rod attains a constant temperature, then
View Solution
Knowledge Check
The two ends of uniform rod of thermal conductivity K are maintained at different but constant temperatre. The temperature gradient at any point on the rod is dθ/dx. The heat flow per unit time per unit cross-section of the rod is I.
(i) dθdx is the same for all point on the rod
(ii) I=KdθdxA(i) onlyB(ii) onlyC(i), (ii)DnoneThe ends of a rod of uniform thermal conductivity are maintained at different (constant) temperatures. Afer the steady state is achieved:
Aheat flows in the rod from high temperature to low temperature even if the rod has nonuniform cross sectional area.Btemperature gradient along length is same even if the rod has non uniform cross sectional area.Cheat current is same even if the rod has nono-uniform cross sectional areaDif the rod has uniform cross sectional area the temperature is same at all points of the rod.Two ends of area A of a uniform rod of thermal conductivity k are maintained at different but constant temperatures. At any point on the rod, the temperature gradient is dTdl. If I be the thermal current in the rod, then:
AI∝ABI∝dTdlCI∝A∘DI∝1(dTdl)
When two ends of a rod wrapped with cotton are maintained at differences and after some time every point of the rod attains a constant temperature, then
View SolutionCurved surface of a uniform rod is isolated from surrounding. Ends of the rod are maintained at temperatures T1 and T2(T1>T2) for a long time. At an instant, temperature T1 starts to decrease at a constant and slow rate. If thermal capacity of material of the rod is considered, then which of thefollowing statements is/are correct ?
View SolutionThe ends of a cylinder steel rod are maintained at two different temperatures. The rod conducts heat from one end to the other at a rate of 10 cal/ s. At what rate would a steel rod twice as long and twice the diameter conduct heat between the same two temperatures?
View SolutionThree metal rods of coefficient of thermal conductivities K,2K,3K conducts heats of 3Q,2Q,Q per seconds through unit area then the ratio of temperature gradients .
View SolutionTwo identical rods with different thermal conductivities k1 & k2 and different temperatures are first placed along length and then along area, then the ratio of rates of heat flow in both cases is
View Solution

