किरण - चित्र की मदद से एक संयुक्त सूक्ष्मदर्शी या खगोलीय दूरबीन दूरबीन द्वारा प्रतिबिम्ब रचना को समझाइए। आपके यंत्र की आवर्द्धन क्षमता के लिए व्यंजक निकालें तथा उसके उपयोगों को बताइए।

Video Solution

Text Solution

Verified by Experts

संयुक्त सूक्ष्मदर्शी में प्रतिबिम्ब का निर्माण -

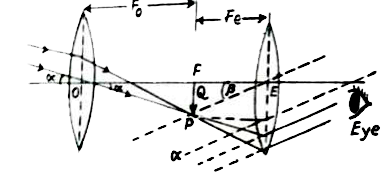
आवर्धन क्षमता - संयुक्त सूक्ष्मदर्शी का कोणीय आवर्धन या आवर्धन क्षमता निम्न तरीके से परिभाषित किया जाता है -
कोणीय अवर्धन या आवर्धन क्षमता, $M = \frac{दूरी पर बन अंतिम प्रतिबिम्ब A B द्वारा नेत्र पर आंतरिक कोण (β)}{उसी दूरी D पर स्थित वस्तु द्वारा नेत्र पर आंतरिक कोण (α)}$
चूँकि $α$ और $β$ कोण बहुत छोटा है।
$α \equiv tan α, β \equiv tan β ∴ M = \frac{tan β}{tan α}$
अब $tan β = \frac{A B}{D} \times \frac{D}{A B} ∴ M = \frac{A B}{A B}$ या $M = \frac{A B}{A . B .} \times \frac{A . B .}{A B}$
$∴ M = M_{e} \times M_{0}$
जहाँ $M e = \frac{A B}{A . B .}$ नन्रिका द्वारा आवर्धन
(a) सामान्य समायोजन के प्रतिबिम्ब का निर्माण

आवर्धन क्षमता - समान समायोजन दूरदर्शक की आवर्धन क्षमता M निम्नलिखित रूप से परिभाषित किया जाता है।
आवर्ध क्षमता या कोणीय आवर्धन , $M = \frac{β}{α}$
चूँकि $α$ और $β$ बहुत छोटा है इसलिए $α \equiv tan α, β \equiv tan β$
$∴ M = \frac{tan β}{tan α}$
माना I वस्तु का प्रतिबिम्ब है तथा $f_{0}$ , और $f e$ क्रमशः अभिदृश्यक और नेत्रिका की फोकस दूरियाँ है।
अतः $tan α = \frac{I}{f_{0}}$ और $tan β = \frac{- 1}{f_{e}} ∴ M = \frac{\frac{I}{f_{e}}}{\frac{I}{f_{0}}} = \frac{f_{0}}{f_{e}}$ या $M = \frac{f_{0}}{f_{e}}$
(b) स्पष्ट दिष्टि की न्यूनतम दूरी पर अंतिम प्रतिबिम्ब का बनना

आवर्धन क्षमता - समान समायोजन दूरदर्शन की आवर्धन क्षमता M निम्नलिखित रूप से अंकित किया जाता है।
आवर्धन क्षमता $M = \frac{β}{α}$
चूँकि $α$ और $β$ बहुत छोटा है
अतः $α \equiv tan α, β \equiv tan β, M = \frac{tan β}{tan α}$ .....(i)
In $Δ A . B . C_{2} tan β = \frac{A . B .}{C_{2} B .}$
In $Δ A . B . C_{2}, tan α = \frac{A . B .}{C_{1} B .}$
समी. (i) से, $M = \frac{A . B .}{C_{2} B .} \times \frac{C_{1} B .}{A . B .}$
या $M = \frac{C_{1} B .}{C_{2} B .}$
यहाँ $C_{1} B . = + f_{0}$ और $C_{2} B . = - μ_{e}$
$M = \frac{f_{0}}{- u_{e}}$ .....2
अब लेंस सूत्र से , $\frac{1}{v} - \frac{1}{u} = \frac{1}{f}$ (नेत्रिका के लिए)
$\frac{1}{- D} - \frac{1}{- u_{e}} = \frac{1}{f_{e}}$ या, $- \frac{1}{D} + \frac{1}{u_{e}} = \frac{1}{f_{e}}$
या, $\frac{1}{u_{e}} = \frac{1}{f_{e}} + \frac{1}{D}$ या, $\frac{f_{0}}{u_{e}} = \frac{f_{0}}{f_{e}} + \frac{1}{D}$
या, $\frac{f_{0}}{u_{e}} = \frac{f_{0}}{f_{e}} (1 + \frac{f_{e}}{D})$ या, $- \frac{f_{0}}{u_{e}} = - \frac{f_{0}}{f_{e}} (1 + \frac{f_{e}}{D})$
समी. (ii)से $M = \frac{- f_{0}}{f_{e}} (1 + \frac{f_{e}}{D})$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

BIHAR BOARD- PREVIOUS YEAR PAPER-भौतिक विज्ञान -2009-खण्ड-II (गैर-वस्तुनिष्ट प्रश्न )(दीर्घ उत्तरीय प्रश्न)

Home
Ask Doubt
Profile