किसी विद्युत द्विध्रुव के कारण क्षेत्र एवं विभव के बीच अवकल सम्बध द्वारा विद्युत विभव एवं विद्युत क्षेत्र ज्ञात करें।

Video Solution

Text Solution

Verified by Experts

विद्युत द्विध्रुव के कारण किसी बिन्दु पर विद्युतीय विभव का व्यंजक - मान लिया कि AB एक विद्युतीय - द्विध्रुव है जिसके विजातीय आवेश +Q तथा -Q एक दूसरे से अल्पदूरी 2I पर स्थित है। द्विध्रुव के कारण किसी बिन्दु P पर विद्युत विभव का मान ज्ञात करना है । जिसके ध्रुवीय केंद्र O के सापेक्ष $(r, θ)$ है , अर्थात OP= r तथा $∠ P O A = θ$ बिन्दु A से PO पर खींचा गया लंब AN है इसी प्रकार बिन्दु B से बड़ी गयी रेखा PO पर खींचा गया लंब BM है , जैसा कि नीचे चित्र में दिखाया गया है।

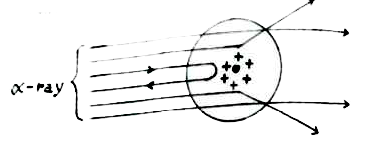
अब समकोण $Δ A O N$ में $O N = O A cos θ = l cos θ$
और समकोण $Δ B O M$ में, $O M = O B cos θ = l cos θ$
अब चूँकि दोनों आवेगों के बीच की दूरी 2l बहुत कम है इसलिए PA लगभग PN के तथा PB लगभग PM बराबर होंगें । अतः $P A = P N = P O - O N = r - l cos θ$
और $P B = P M = P O + O M = r + l cos θ$
A पर स्थित +Q आवेग के कारण P बिन्दु पर विभव $V_{1} = + \frac{1}{4 ε_{0}} \frac{Q}{P A} = + \frac{1}{4 π ε_{0}} \frac{Q}{(r - l cos θ)}$
तथा B पर स्थित Q आवेग के कारण P बिन्दु पर विभव
$1 = \frac{1}{4 π ε_{0}} \frac{Q}{P B} = - \frac{1}{4 π ε_{0}} \frac{Q}{(r - l cos θ)}$
P पर द्विध्रुव के कारण परिणाम विभव
$V = V_{1} + V_{2} = \frac{Q}{4 π ε_{0}} [\frac{1}{r - l cos θ} - \frac{1}{(r + l cos θ)}] = \frac{Q}{4 π ε_{0}} [\frac{r + l cos - r + l cos θ}{(r^{2} - l^{2} cos θ)}] = \frac{Q}{4 π ε_{0}} \frac{2 l cos θ}{(r^{2} - l^{2} {cos}^{2} θ)} = \frac{1}{4 π ε_{0}} \frac{P cos θ}{(r^{2} - l^{2} {cos}^{2} θ)}$ ...(i)
जहाँ $P = θ \times 2 l$ , द्विध्रुव का आघूर्ण है फिर चूँकि $r^{2}$ की तुलना में $l^{2} {cos}^{2} θ$ का मान साम्य है। इसलिए समी (i) से P पर विभव
$V = \frac{1}{4 π ε_{0}} \frac{P cos θ}{r^{2}}$
यदि $ˆ r . O P$ की दिशा में एकांक सदिश हो तो
$\to P . ˆ r = P \times l cos θ = P cos θ$
अतः समी (ii) को सदिश संकेत में हम इस प्रकार व्यक्त कर सकते है।
$V = \frac{1}{4 π ε_{0}} . \frac{\to P . ˆ r}{r^{2}}$ .
कलन विधि द्वारा विद्युत क्षेत्र का परिकलन निम्न है - माना AB एक विद्युतीय - द्विध्रुव है। जिसके आवेग +Q तथा -Q के बीच की दूरी 2I है इसके मध्यबिन्दु O से r दूरी पर कोई बिन्दु P है। जहाँ विद्युत क्षेत्र की तीव्रता का मान निकालना है।
अगर बिन्दु P पर विद्युतीय विभव का मान v है तो $V = \frac{1}{4 π ε_{0}} . \frac{P cos θ}{r^{2}}$

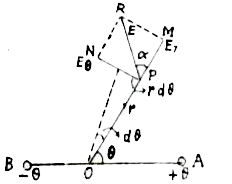
चित्र में स्पष्ट है कि OP दिशा में दूरी का परिवर्तन dr तथा उसके लंबवत PN दिशा में कोई परिवर्तन rd $θ$ है। अब $E r = \frac{d r}{d r} = \frac{d}{d t} [\frac{1}{4 π ε_{0}} \frac{P cos θ}{r^{2}}]$
$= \frac{- 1}{4 π ε_{0}} P cos θ \frac{d}{d r} (\frac{1}{r^{2}}) = - \frac{1}{4 π ε_{0}} P cos θ (- \frac{2}{r^{3}})$
$E r = - \frac{1}{4 π ε_{0}} \frac{2 p cos θ}{r^{3}}$ तथा $E_{0} = - \frac{1}{r} \frac{\partial v}{\partial θ} = - \frac{1}{r} \frac{\partial}{\partial θ} (\frac{1}{4 π ε_{0}} \frac{P cos θ}{r^{2}})$
$= - \frac{1}{4 π ε_{0}} \frac{P}{r^{3}} (\frac{d cos θ}{d θ}) = - \frac{1}{4 π ε_{0}} \frac{P}{r^{3}} (- sin θ)$
$∴ E_{θ} = \frac{1}{4 π ε_{0}} \frac{Ψ n θ}{r^{3}}$
$E = \sqrt{E r^{2} + E_{θ}} = \frac{1}{4 π ε_{0}} \frac{P}{r^{3}} (\sqrt{4 {cos}^{2} θ + {sin}^{2} θ})$
$E = \frac{1}{4 π ε_{0}} \frac{P}{r^{3}} \sqrt{1 + 3 {cos}^{2} θ}$

Updated on:21/07/2023

|

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

BIHAR BOARD- PREVIOUS YEAR PAPER-भौतिक विज्ञान -2009-खण्ड-II (गैर-वस्तुनिष्ट प्रश्न )(दीर्घ उत्तरीय प्रश्न)

Home
Ask Doubt
Profile