Question

A particel which is simultaneously subjected to two perpendicular simple harmonic motions represented by ${\displaystyle x=a_1\cos \omega t}$ and ${\displaystyle y=a_2\cos 2\omega t}$ traces a curve given by :

Options

A.
B.
C.
D.

Answer

A

Explanation

To solve the problem of finding the curve traced by a particle subjected to two perpendicular simple harmonic motions represented by $$x=a_1\cos \left(\omega t\right)$$ and $$y=a_2\cos \left(2\omega t\right)$$, we will follow these steps:

Step 1: Understand the given equations
We have two equations:
- \( x = a_1 \cos(\omega t) \)
- \( y = a_2 \cos(2\omega t) \)

Step 2: Express \( \cos(2\omega t) \) in terms of \( \cos(\omega t) \)
Using the double angle formula for cosine:
\( \cos(2\theta) = 2\cos^2(\theta) - 1 \)
we can write:
\( \cos(2\omega t) = 2\cos^2(\omega t) - 1 \)

Step 3: Substitute \( \cos(\omega t) \) in terms of \( x \)
From the first equation, we can express \( \cos(\omega t) \):
\( \cos(\omega t) = \frac{x}{a_1} \)
Now substituting this into the expression for \( \cos(2\omega t) \):
\( \cos(2\omega t) = 2\left(\frac{x}{a_1}\right)^2 - 1 = \frac{2x^2}{a_1^2} - 1 \)

Step 4: Substitute into the equation for \( y \)
Now we substitute this back into the equation for \( y \):
\( y = a_2 \left(2\left(\frac{x}{a_1}\right)^2 - 1\right) \)
This simplifies to:
\( y = a_2 \left(2\frac{x^2}{a_1^2} - 1\right) = \frac{2a_2}{a_1^2} x^2 - a_2 \)

Step 5: Rearrange the equation
Rearranging gives us:
\( y + a_2 = \frac{2a_2}{a_1^2} x^2 \)
This can be rewritten as:
\( \frac{2a_2}{a_1^2} x^2 = y + a_2 \)

Step 6: Identify the type of curve
The equation \( \frac{2a_2}{a_1^2} x^2 = y + a_2 \) is in the form of a parabola, specifically:
\( x^2 = \frac{a_1^2}{2a_2}(y + a_2) \)
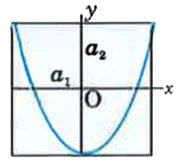
This shows that the curve is a parabola that opens upwards.

Conclusion
The curve traced by the particle is a parabola symmetric about the y-axis.

---