A particle which is simultaneously subjected to two perpendicular simple harmonic motions represented by , x=a1coscot and y=a2cos2cot traces a curve given by:




To solve the problem of a particle subjected to two perpendicular simple harmonic motions represented by x=a1cos(ωt) and y=a2cos(2ωt), we can follow these steps:
Step 1: Write the equations for x and y
We start with the given equations:
x=a1cos(ωt)(1)
y=a2cos(2ωt)(2)
Step 2: Express cos(2ωt) in terms of cos(ωt)
Using the double angle identity for cosine, we know that:
cos(2θ)=2cos2(θ)−1
Applying this to our case, we have:
cos(2ωt)=2cos2(ωt)−1
Substituting this into equation (2):
y=a2(2cos2(ωt)−1)
Step 3: Substitute cos(ωt) from equation (1)
From equation (1), we can express cos(ωt) as:
cos(ωt)=xa1
Now substituting this into the expression for y:
y=a2(2(xa1)2−1)
Step 4: Simplify the equation for y
Expanding the equation gives:
y=a2(2x2a21−1)
This can be rearranged to:
y=2a2a21x2−a2
Step 5: Rearranging to standard form
Rearranging the equation, we get:
2a2a21x2−y−a2=0
This can be rewritten as:
x2a212a2−ya2=1
This is the standard form of a hyperbola.
Conclusion
Thus, the curve traced by the particle is a hyperbola.
---
We start with the given equations:
x=a1cos(ωt)(1)
y=a2cos(2ωt)(2)
Using the double angle identity for cosine, we know that:
cos(2θ)=2cos2(θ)−1
Applying this to our case, we have:
cos(2ωt)=2cos2(ωt)−1
Substituting this into equation (2):
y=a2(2cos2(ωt)−1)
From equation (1), we can express cos(ωt) as:
cos(ωt)=xa1
Now substituting this into the expression for y:
y=a2(2(xa1)2−1)
Expanding the equation gives:
y=a2(2x2a21−1)
This can be rearranged to:
y=2a2a21x2−a2
Rearranging the equation, we get:
2a2a21x2−y−a2=0
This can be rewritten as:
x2a212a2−ya2=1
This is the standard form of a hyperbola.
Thus, the curve traced by the particle is a hyperbola.
Similar Questions
A particle is acted simultaneously by mutually perpendicular simple harmonic motion x=acosωt and y=asinωt. The frequency of motion of the particle will be
View SolutionA particle is acted simultaneously by mutually perpendicular simple hormonic motions x=acosωtandy=asinωt. The trajectory of motion of the particle will be
View Solution
Knowledge Check
A particel which is simultaneously subjected to two perpendicular simple harmonic motions represented by x=a1cosωt and y=a2cos2ωt traces a curve given by :
A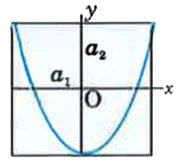 B
B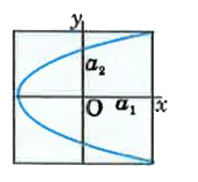 C
C D
D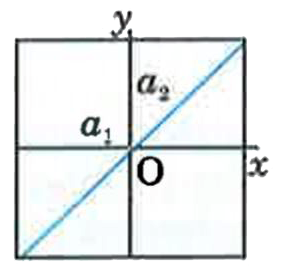
A particle isolated simultaneously by mutually perpendicular simple harmonic motion x = a cos ωt and y = a sin ωt. The trajectory of motion of the particle will be:
AAn ellipseBA parabolaCA circleDA straight lineA particle is acted simultaneously by mutually perpendicular simple harmonic motions x=a cosωt and y=asinωt. The trajectory of motion of the particle will be
Aan ellipseBa parabolaCa circleDa straight line.
A particle is acted simultaneously by mutally perpendicular simple harmonic motion x=acosωt and y=asinωt. The trajectory of motion of the particle will be
View SolutionA particle is subjected to two mutually perpendicualr simple harmonic motions such that its x and y-coordinates are given by
x=sinωt, y=2cosωt
The path of the particle will be :
View SolutionA particle is subjected to two mutually perpendicular simple harmonic motions such that its X and y coordinates are given by X=2sinωt , y=2sin(ω+π4)
The path of the particle will be:
View SolutionA particle is subjected to two mutually perendicular simple harmonic motion such that its x and y coordinates are given by :
x=2sinω & y=2sin(ωt+π2)
The path of the particle will be
View SolutionWhat is the phase difference between two simple harmonic motions represented by x1=Asin(ωt+π6) and x2=Acos(ωt)?
View Solution
