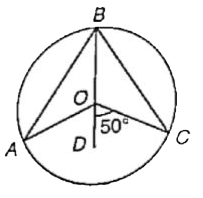
'O' is the centre of the circle, line segment BOD is the angle bisector of ∠AOC,∠COD=50∘. Find ∠ABC :
25∘
50∘
100∘
120∘
The correct Answer is:B
Step by step video, text & image solution for 'O' is the centre of the circle, line segment BOD is the angle bisector of angleAOC, angleCOD = 50^(@). Find angleABC : by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - EXERCISE(LEVEL 1)
54 Videos
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - EXERCISE(LEVEL 2)
52 Videos
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.4
10 Videos
- FUNDAMENTALS BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - TEST OF YOU - LEARNING - 2
40 Videos
- HCF AND LCMBOOK - ARIHANT SSCCHAPTER - HCF AND LCMEXERCISE - Exercise Higher Skill Level Questions
18 Videos
Similar Questions
Knowledge Check
'O' is the centre of the circle, line segment BOD is the angle bisector of ∠AOC,∠COD=50∘. Find ∠ABC :
 A25∘B50∘C100∘D120∘
A25∘B50∘C100∘D120∘If O is the centre of the circle then find ∠ADC
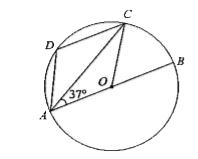 A125∘B127∘C90∘D137∘
A125∘B127∘C90∘D137∘O is the centre of the circle, ABN is a straight line. Find ∠AOC.
 A128∘B132∘C130∘D135∘
A128∘B132∘C130∘D135∘
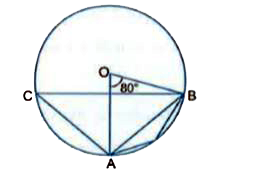
In the following figure, O is the centre of the circle. AB is an arc of the circle, such that ∠AOB=80∘.Find ∠ACB.
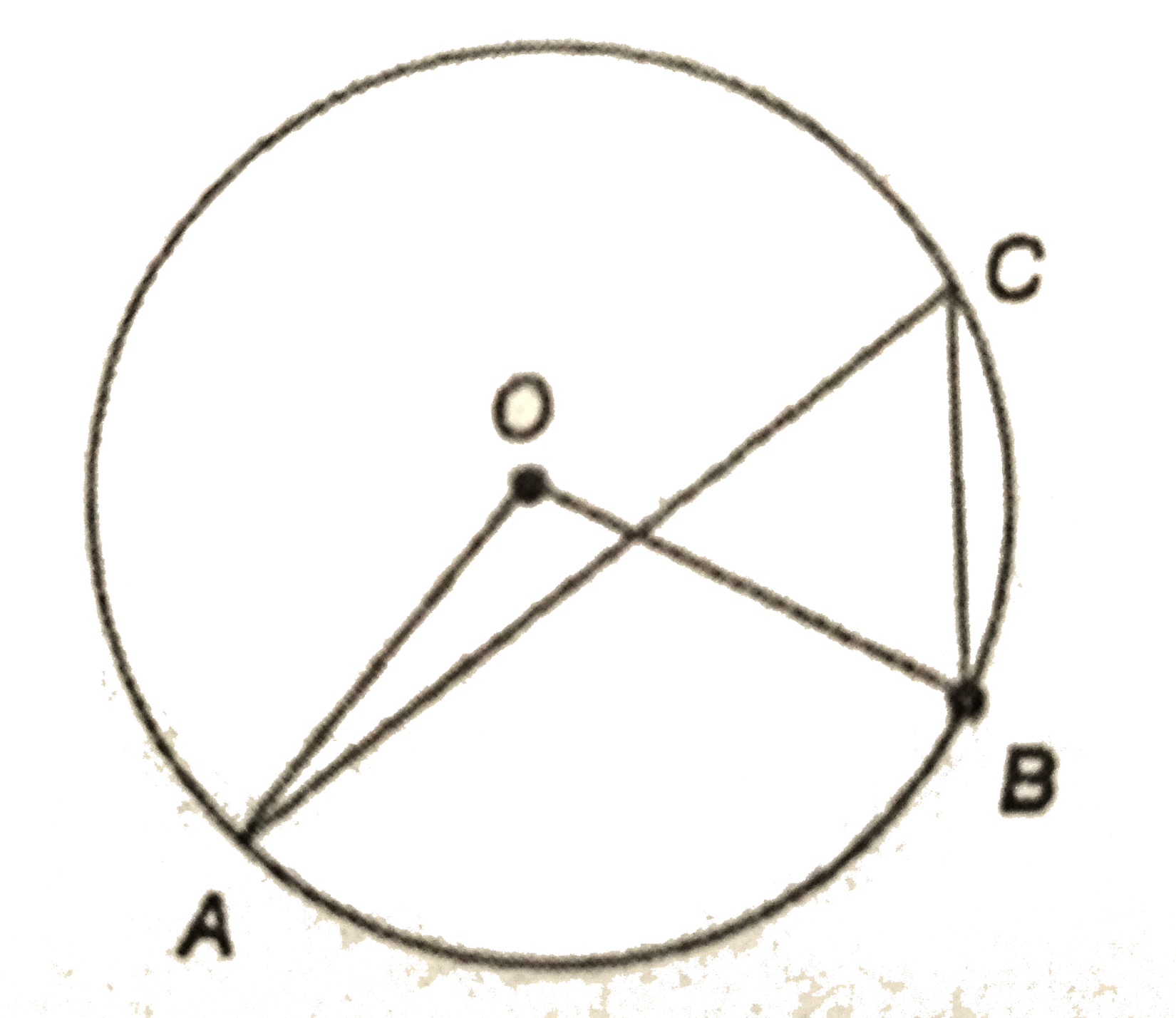
View SolutionIn Figure, O is the centre of the circle. If ∠BOD=1600, find the values of x and y
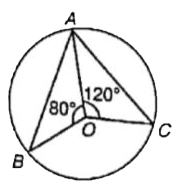
View SolutionIn the given figure, O is the centre of circle. ∠AOC=120∘. Find ∠BAC :
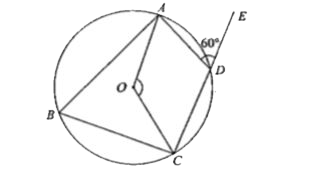
View SolutionIf O is the centre of circle and ∠ADE=60∘ then find ∠AOC
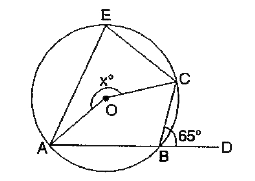
View SolutionIn the given figure, O is the centre of the circle. ABD is a straight line and ∠CBD=65∘. Find reflex ∠AOC (marked x∘).
View Solution