If AB is a chord of a circle, P and Q are two points on the circle different from A and B, then:
the angle subtended by AB at P and Q are either equal or supplementary.
the sum of the angles subtended by AB at P and Q alwasys equal two right angles.
the angles subtended at P and Q by AB are always equal.
the sum of the angles subtended at P and Q is equal to four right angles.
The correct Answer is:A
To solve the problem, we need to analyze the properties of angles subtended by a chord in a circle. Here’s a step-by-step breakdown of the solution:
Step 1: Draw the Circle and Chord
Draw a circle and label it. Identify a chord within the circle and label the endpoints of the chord as points A and B.
Hint: Remember that a chord is a straight line connecting two points on the circumference of a circle.
Step 2: Identify Points on the Circle
Select two additional points on the circumference of the circle, labeling them as points P and Q. Ensure that P and Q are distinct from points A and B.
Hint: The points P and Q should be anywhere on the circumference, but not on the chord itself.
Step 3: Draw Angles
Draw line segments from point A to point P and from point B to point P. This creates angle APB. Similarly, draw line segments from point A to point Q and from point B to point Q, creating angle AQB.
Hint: The angles APB and AQB are formed by the chord AB and the lines connecting A and B to points P and Q.
Step 4: Analyze the Angles
According to the properties of circles, the angles subtended by the same chord (AB) at any point on the circumference (P and Q) are equal. Therefore, angle APB is equal to angle AQB.
Hint: Recall the theorem that states the angle subtended by a chord at any point on the circumference is the same.
Step 5: Conclusion
Since the angles APB and AQB are equal, we conclude that the correct statement from the options provided is that the angles subtended at points P and Q by chord AB are always equal.
Final Answer: The correct option is 3: "The angle subtended at P and Q by AB are always equal."
Draw a circle and label it. Identify a chord within the circle and label the endpoints of the chord as points A and B.
Select two additional points on the circumference of the circle, labeling them as points P and Q. Ensure that P and Q are distinct from points A and B.
Draw line segments from point A to point P and from point B to point P. This creates angle APB. Similarly, draw line segments from point A to point Q and from point B to point Q, creating angle AQB.
According to the properties of circles, the angles subtended by the same chord (AB) at any point on the circumference (P and Q) are equal. Therefore, angle APB is equal to angle AQB.
Since the angles APB and AQB are equal, we conclude that the correct statement from the options provided is that the angles subtended at points P and Q by chord AB are always equal.
Topper's Solved these Questions
- GEOMETRYBook:ARIHANT SSCChapter:GEOMETRYExercise:EXERCISE(LEVEL 1)
Explore 54 Videos
- GEOMETRYBook:ARIHANT SSCChapter:GEOMETRYExercise:EXERCISE(LEVEL 2)
Explore 52 Videos
- GEOMETRYBook:ARIHANT SSCChapter:GEOMETRYExercise:INTRODUCTORY EXERCISE - 12.4
Explore 10 Videos
- FUNDAMENTALS Book:ARIHANT SSCChapter:FUNDAMENTALS Exercise:TEST OF YOU - LEARNING - 2
Explore 40 Videos
- HCF AND LCMBook:ARIHANT SSCChapter:HCF AND LCMExercise:Exercise Higher Skill Level Questions
Explore 18 Videos
Similar Questions
If AB is a chord of a circle, Pand Q are the two points on the circle different from A and B, then ∠APB= ∠AQB ∠APB+∠AQB=180∘ or∠APB= ∠AQB
View SolutionAB is a chord of a circle with O as centre. C is a point on the circle such that OC is perpendicular to AB and OC intersects AB at P. If PC = 2 cm and AB = 6 cm then the diameter of the circle is
View Solution
Knowledge Check
A point charge q is held at the centre of a circle of radius r. B,C are two points on the circumference of the circle and A is a point outsdie the circle . If WAB charge qe from A to B and WAC represents the workdone from A to C ,then
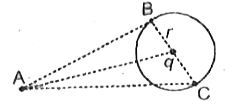 AWAB>WACBWAB<WACCWAB=WAC≠0DWAB=WAC=0
AWAB>WACBWAB<WACCWAB=WAC≠0DWAB=WAC=0AB is a chord to a circle and PAT is the tangent to the circle at A. If ∠BAT=75∘and∠BAC=45∘, C being a point on the circle, then ∠ABC is equal to
A40∘B45∘C60∘D70∘If a chord AB subtends and angle of 60∘ at the centre of a circle, then the angle between the tangents to the circle drawn from A and B is
A30∘B60∘C90∘D120∘
AB is a diameter of a circle. P is a point on the semi-circle APB.AHandBK are perpendiculars from AandB respectively to the tangent at P. Prove that AH+BK=AB.
View SolutionPA and PB are two tangents to a circle with centre O, from a point P outside the circle. A and B are points on the circle. If ∠APB=40∘, then ∠OABis equal to:
View SolutionPA and PB are two tangents to a circle with centre O, from a point P outside the circle . A and B are point P outside the circle . A and B are point on the circle . If ∠PAB=47∘ , then ∠OAB is equal to :
View SolutionPA and PB are two tangents to a circle with centre 0. from a point P outside the circle. A and B are points on the circle. If ∠APB=70∘ then ∠OAB is equal to:
View SolutionPA and PB are two tangents to a circle with centre O, from a point P outside the circle. A and B are points on the circle. If ∠APB=100∘ , then OAB is equal to:
View Solution
