If AB is a chord of a circle, Pand Q are the two points on the circle different from A and B, then ∠APB= ∠AQB ∠APB+∠AQB=180∘ or∠APB= ∠AQB
Video Solution
Text Solution
∠APB=∠AQB
AB is chord of a circle
Pand Q are two points other than from points Aand B
∠APBand∠AQB
are in the same segment of the circle
∠APB=∠AQB
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
If AB is a chord of a circle, P and Q are two points on the circle different from A and B, then:
Athe angle subtended by AB at P and Q are either equal or supplementary.Bthe sum of the angles subtended by AB at P and Q alwasys equal two right angles.Cthe angles subtended at P and Q by AB are always equal.Dthe sum of the angles subtended at P and Q is equal to four right angles.If AB is a chord of a circle, P and Q are two points on the circle different from A and B, then:
Athe angle subtended by AB at P and Q are either equal or supplementaryBthe sum of the angles subtended by AB at P and q is always equal two right anglesCthe angles subtended at P and Q by AB are always equalDthe sum of the angles subtended at P and q is equal to four right anglesIn a △ABC,if 2∠A=3∠B=6∠C, then ∠B=?
A30∘B45∘C60∘D90∘
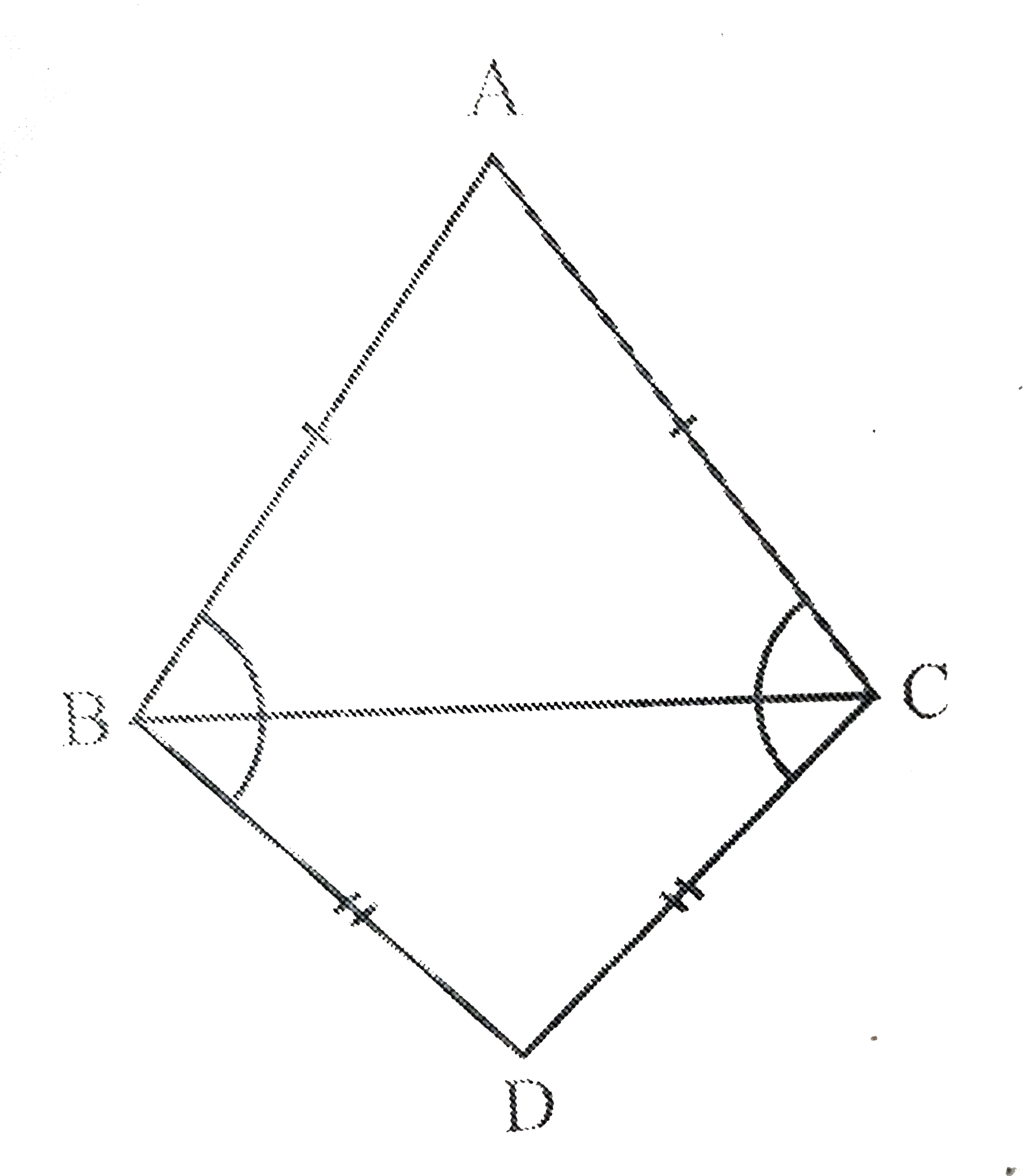
ABC and DBC are two isosceles triangles on the same base BC (see Fig. 7.33). Show that∠ABD =∠ACD
View Solutionline l is the bisector of an angle ∠A and∠Bis any point on l. BP and BQ are perpendiculars from B to the arms of ∠A. Show that:
(i) ΔAPB≅ΔAQB
(ii) BP = BQ or B is equidistant from the arms of ∠A

View SolutionIn Figure, line l is the bisector of angle A and B is any point on l . BP and BQ are perpendiculars from B to the arms of A. Show that : APB≅AQB BP=BQ or B is equidistant from the arms of ∠A . Figure
View SolutionIn △ABC,if∠A=65∘ and ∠C=85∘, then ∠B = ?
View SolutionIn a ΔABC,∠A+∠B=70∘ and ∠B+∠C=130∘, value of ∠A is
View Solution

