A point X inside a rectangle PQRS is joined to the vertices then, which of the following is true:
A(ΔPSX)=A(ΔRXQ)
A(ΔPSX)+A(ΔPXQ)=A(ΔRSX)+A(ΔRQX)
A(ΔPXS)+A(ΔRXQ)=A(ΔSRX)+A(ΔPXQ)
none of these
The correct Answer is:C
To solve the problem, we need to analyze the areas of triangles formed by point X inside rectangle PQRS.
1. Identify the Rectangle and Point:
- We have a rectangle PQRS with vertices P, Q, R, and S.
- Let X be a point inside the rectangle.
2. Understanding Triangle Areas:
- When point X is connected to the vertices of the rectangle, it creates four triangles:
- Triangle PSX
- Triangle QSX
- Triangle RXQ
- Triangle PXQ
3. Using the Area Relationship:
- The key property we will use is that the area of triangles that share a common base and height can be compared.
- The area of triangle PSX is opposite to the area of triangle RXQ, and the area of triangle PXQ is opposite to the area of triangle QSX.
4. Setting Up the Equation:
- According to the properties of triangles formed by a point inside a rectangle, we can state:
Area of △PSX+Area of △RXQ=Area of △QSX+Area of △PXQ
5. Analyzing the Options:
- Now, we can check the options given in the question:
- Option 1: Area of triangle PSX = Area of triangle RXQ (not true)
- Option 2: Area of triangle PSX + Area of triangle PXQ = Area of triangle RSX + Area of triangle RXQ (not true)
- Option 3: Area of triangle PSX + Area of triangle RXQ = Area of triangle RSX + Area of triangle PXQ (this is true)
- Option 4: None of these (not applicable)
6. Conclusion:
- The correct statement is that the area of triangle PSX plus the area of triangle RXQ is equal to the area of triangle QSX plus the area of triangle PXQ.
Final Answer:
The correct option is Option 3: Area of triangle PSX + Area of triangle RXQ = Area of triangle QSX + Area of triangle PXQ.
- We have a rectangle PQRS with vertices P, Q, R, and S.
- Let X be a point inside the rectangle.
- When point X is connected to the vertices of the rectangle, it creates four triangles:
- Triangle PSX
- Triangle QSX
- Triangle RXQ
- Triangle PXQ
- The key property we will use is that the area of triangles that share a common base and height can be compared.
- The area of triangle PSX is opposite to the area of triangle RXQ, and the area of triangle PXQ is opposite to the area of triangle QSX.
- According to the properties of triangles formed by a point inside a rectangle, we can state:
Area of △PSX+Area of △RXQ=Area of △QSX+Area of △PXQ
- Now, we can check the options given in the question:
- Option 1: Area of triangle PSX = Area of triangle RXQ (not true)
- Option 2: Area of triangle PSX + Area of triangle PXQ = Area of triangle RSX + Area of triangle RXQ (not true)
- Option 3: Area of triangle PSX + Area of triangle RXQ = Area of triangle RSX + Area of triangle PXQ (this is true)
- Option 4: None of these (not applicable)
- The correct statement is that the area of triangle PSX plus the area of triangle RXQ is equal to the area of triangle QSX plus the area of triangle PXQ.
The correct option is Option 3: Area of triangle PSX + Area of triangle RXQ = Area of triangle QSX + Area of triangle PXQ.
Topper's Solved these Questions
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.4
10 Videos
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.5
60 Videos
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.2
100 Videos
- FUNDAMENTALS BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - TEST OF YOU - LEARNING - 2
40 Videos
- HCF AND LCMBOOK - ARIHANT SSCCHAPTER - HCF AND LCMEXERCISE - Exercise Higher Skill Level Questions
18 Videos
Similar Questions
A point O inside a rectangle ABCD is joined to the vertices. Prove that the sum of the areas of a pair of opposite triangles so formed is equal to the sum of the other pair of triangles. Given: A rectangle ABCDandO is a point inside it. OA,OB,OCandOD have been joined. To Prove: ar(AOD)+ar(BOC)=ar(AOB)+ar(COD)
View SolutionA point O inside a rectangle ABCD is joined to the vertices. Prove that the sum of the areas of a pair of opposite triangles so formed is equal to the sum of the other pair of triangles. GIVEN : A rectangle ABCD and O is a point inside it. OA,OB,OC and OD have been joined.. TO PROVE : ar(AOD)+ar(BOC)=ar(AOB)+ar(COD) CONSTRUCTION : Draw EOFAB and LOMAD.
View Solution
Knowledge Check
STOP is a rectangle STAR is a parallelogram in the given figure.
Which of the following statement is true ?
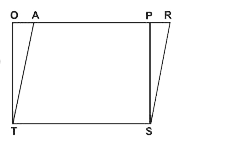 APerimeter (STAR) > Perimeter (STOP)BPerimeter (STAR) < Perimeter (STOP)CPerimeter (STAR)= Perimeter (STOP)DPerimeter (STAR) =12 Perimeter (STOP)
APerimeter (STAR) > Perimeter (STOP)BPerimeter (STAR) < Perimeter (STOP)CPerimeter (STAR)= Perimeter (STOP)DPerimeter (STAR) =12 Perimeter (STOP)If in two triangles ABC and PQR, ABQR=BCPR , then which of the following is true?
AΔBCA~ΔPQRBΔPQR~ΔCABCΔPQR~ΔABCDΔCBA~ΔPORIf the vertices P,Q,R of a triangle PQR are rational points, which of the following points of the triangle PQR is (are) always rational points(s)?
AcentroidBincentreCcircumcentreDorthocentre
In the figure, a point O inside △ABC is joined to its vertices. From a point D on AO, DE is drawn parallel to AB and from a point E on BO, EF is drawn parallel to BC. Prove that DF || AC.
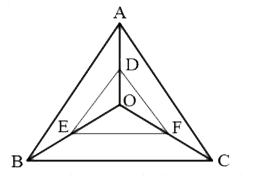
View SolutionA point O in the interior of a rectangle ABCD is joined with each of the vertices A, B, C and D . Prove that OB2+OD2=OC2+OA2
View SolutionAny point X inside DEF is joined to its vertices. From a point P in DX, PQ is drawn parallel to DE meeting XE at Q and QR is drawn parallel to EF meeting XF in R . Prove that PRDF .
View SolutionIf the vertices P,Q,R of a triangle PQR are rational points, which of the following points of thetriangle PQR is/are always rational point(s) ?(A) centroid(B) incentre(C) circumcentre(D) orthocentreAgrawn Korouteden36
View SolutionWhich of the following is true if △PQR≅△SET?
View Solution
