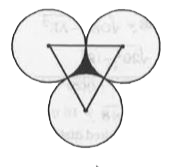
Three circle of equal radii touch each other as shown in figure . The radius of each circle is 1 cm. What is the area of shaded region ?
(2√3−π2)cm2
(3√2−π3)cm2
2√3πcm2
none of the above
The correct Answer is:A
Step by step video, text & image solution for Three circle of equal radii touch each other as shown in figure . The radius of each circle is 1 cm. What is the area of shaded region ? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MENSURATIONBook:ARIHANT SSCChapter:MENSURATIONExercise:EXERCISE (LEVEL 2)
Explore 68 Videos
- MENSURATIONBook:ARIHANT SSCChapter:MENSURATIONExercise:TEST OF YOUR LEARNING
Explore 18 Videos
- MENSURATIONBook:ARIHANT SSCChapter:MENSURATIONExercise:EXERCISE (MISCELLANEOUS)
Explore 59 Videos
- LOGARITHM Book:ARIHANT SSCChapter:LOGARITHM Exercise:EXERCISE LEVEL 2
Explore 19 Videos
- MIXED GRAPHBook:ARIHANT SSCChapter:MIXED GRAPHExercise:Higher Skill Level Questions
Explore 15 Videos
Similar Questions
Knowledge Check
Three equal circles of unit radius touch each other. Then, the area of the circles is
Aπ3(2+√3)3B2π3(2+√3PP2)C6π(2+√3)2D16π(2+√3)2In the given figure there are 3 semicircles , the radii of each smaller circle is equal. If the radius of the larger circle be 22 cm , then the area of the shaded region is :
 A363π4B363π3C236.5πD363π
A363π4B363π3C236.5πD363πThree equal circles of unit radius touch each other. Then, the area of the circle circumscribing the three circles is:
A6π(2+√3)2Bπ6(2+√3)2Cπ3(2+√3)2D3π(2+√3)2
In the figure, radius of the circle is 14 cm, then the shaded area is
View SolutionThree circles of equal radius 'a' cm touch each other. The area of the shaded region is :
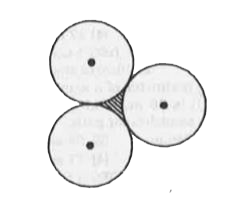
View SolutionThree circles of equal radius 'a' cm touch each other. The area of of the shaded region is :

View SolutionThree equal circles of unit radius touch each other. Then, the area of the circle circumscribing the three circles is:
View SolutionThree circles with equal radii touch each other externally. The figure formed by joining the centres of these circles is
View Solution