King Dashratha of Ayodhya had a rectangular plot of area 9792m2. He divided it into 4 square shaped plots by fencing parallel fences to the breadth of the rectangular plot. All the four sons got each square shaped plot. However , same area of plot was still left which could not be formed as a square shaped. So, four more square shaped plots were formed by fencing parallel to the longer side of the original plot. The king gave one smaller square shaped plot to each of his wives and one of the smaller square shaped plot retained with himself and then nothing left to divide .
What are dimensions of the original plot ?
288 m, 34 m
102 m , 96 m
306 m , 32 m
204 m , 48 m
The correct Answer is:D
To find the dimensions of the original rectangular plot owned by King Dashratha, we will follow these steps:
Step 1: Understand the problem
The area of the rectangular plot is given as 9792m2. The plot is divided into square plots, and we need to find the dimensions (length and breadth) of the original rectangular plot.
Step 2: Set up the equations
Let the side length of each square plot be x. Since King Dashratha divided the rectangular plot into 4 square plots by fencing parallel to the breadth, the total breadth of the rectangular plot will be 4x.
After that, he formed 4 more square plots by fencing parallel to the length of the original plot. The total length of the rectangular plot will be 17x (4 square plots of length x plus the original length).
Step 3: Write the area equation
The area of the rectangular plot can be expressed as:
Area=Length×Breadth=(17x)×(4x)=68x2
Given that the area is 9792m2, we can set up the equation:
68x2=9792
Step 4: Solve for x2
To find x2, we divide both sides of the equation by 68:
x2=979268
Calculating the right side:
x2=144
Step 5: Find x
Taking the square root of both sides gives:
x=√144=12m
Step 6: Find the dimensions of the rectangular plot
Now, we can find the length and breadth:
- Length L=17x=17×12=204m
- Breadth B=4x=4×12=48m
Conclusion
The dimensions of the original rectangular plot are:
- Length = 204m
- Breadth = 48m
The area of the rectangular plot is given as 9792m2. The plot is divided into square plots, and we need to find the dimensions (length and breadth) of the original rectangular plot.
Let the side length of each square plot be x. Since King Dashratha divided the rectangular plot into 4 square plots by fencing parallel to the breadth, the total breadth of the rectangular plot will be 4x.
The area of the rectangular plot can be expressed as:
Area=Length×Breadth=(17x)×(4x)=68x2
Given that the area is 9792m2, we can set up the equation:
68x2=9792
To find x2, we divide both sides of the equation by 68:
x2=979268
Calculating the right side:
x2=144
Taking the square root of both sides gives:
x=√144=12m
Now, we can find the length and breadth:
- Length L=17x=17×12=204m
- Breadth B=4x=4×12=48m
The dimensions of the original rectangular plot are:
- Length = 204m
- Breadth = 48m
Topper's Solved these Questions
- BOOK - ARIHANT SSCCHAPTER - MENSURATIONEXERCISE - EXERCISE (LEVEL 2)68videos
MENSURATION
- BOOK - ARIHANT SSCCHAPTER - MENSURATIONEXERCISE - TEST OF YOUR LEARNING18videos
MENSURATION
- BOOK - ARIHANT SSCCHAPTER - MENSURATIONEXERCISE - EXERCISE (MISCELLANEOUS)59videos
MENSURATION
- BOOK - ARIHANT SSCCHAPTER - LOGARITHM EXERCISE - EXERCISE LEVEL 219videos
LOGARITHM
- BOOK - ARIHANT SSCCHAPTER - MIXED GRAPHEXERCISE - Higher Skill Level Questions15videos
MIXED GRAPH
Similar Questions
A big rectangular plot of area 4320m2 is divided into 3 square-shaped smaller plots by fencing parallel to the smaller side of the plot. However some area of land was still left as a square could not be formed. So, 3 more square-shaped plots were formed by fencing parallel to the longer side of the original plot such that no area of the plot was left surplus. What are the dimensions of the original plot? 160m×27m (b) 240m×18m (c) 120m×36m (d) 135m×32m
View SolutionThe length of a rectangular plot is 1.5 times the breadth. 20% of its perimeter is 20 metres. The area of the plot is
View Solution
Knowledge Check
- Question 1 - Select One
King Dashratha of Ayodhya had a rectangular plot of area 9792m2. He divided it into 4 square shaped plots by fencing parallel fences to the breadth of the rectangular plot. All the four sons got each square shaped plot. However , same area of plot was still left which could not be formed as a square shaped. So, four more square shaped plots were formed by fencing parallel to the longer side of the original plot. The king gave one smaller square shaped plot to each of his wives and one of the smaller square shaped plot retained with himself and then nothing left to divide .
What is the ratio of the area of larger square shaped plot to the area of the smaller square shaped plot ?AA. 17:1BB. 25:9CC. 16:1DD. can't be determined - Question 2 - Select One
King Dashratha of Ayodhya had a rectangular plot of area 9792m2. He divided it into 4 square shaped plots by fencing parallel fences to the breadth of the rectangular plot. All the four sons got each square shaped plot. However , same area of plot was still left which could not be formed as a square shaped. So, four more square shaped plots were formed by fencing parallel to the longer side of the original plot. The king gave one smaller square shaped plot to each of his wives and one of the smaller square shaped plot retained with himself and then nothing left to divide .
What is the ratio of the area of larger square shaped plot to the area of the smaller square shaped plot ?A17:1B25:9C16:1Dcan't be determined - Question 3 - Select One
King Dashratha of Ayodhya had a rectangular plot of area 9792m2. He divided it into 4 square shaped plots by fencing parallel fences to the breadth of the rectangular plot. All the four sons got each square shaped plot. However , same area of plot was still left which could not be formed as a square shaped. So, four more square shaped plots were formed by fencing parallel to the longer side of the original plot. The king gave one smaller square shaped plot to each of his wives and one of the smaller square shaped plot retained with himself and then nothing left to divide .
What are dimensions of the original plot ?A288 m, 34 mB102 m, 96 mC306 m, 32 mD204 m, 48 m
The given shape is divided into a square and two rectangles.
What is the area of the given shape ?
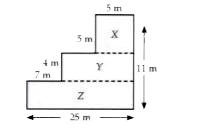 View Solution
View SolutionThe given shape is divided into a square and two rectangles.
What is the area of square X ?
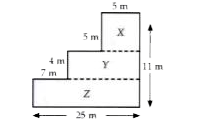 View Solution
View SolutionThe perimeter of a rectangular plot of land is 80 m and its breadth is 16 m . Find the length and area of the plot .
View SolutionTwo plots of land have the same perimeter. One is a square of side 64m and the other is rectangle of length 70m. Find the breadth of the rectangular plot. Which plot has the greater area and by how much?
View SolutionWhat is the area of the rectangular plot?
I. The length of the plot is 375 m.
II. The length of the plot is thrice its breadthView Solution
