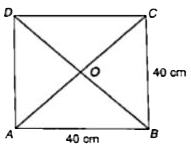
Adjoining figure shows a square ABCD in which O is the point of intersections of diagonals AC and BD . Four squares of maximum possible area are formed inside each four triangles AOB , BOC , COD and AOD . What is the total area of these 4 squares ?
400cm2
100cm2
80cm2
none of these
The correct Answer is:D
Step by step video, text & image solution for Adjoining figure shows a square ABCD in which O is the point of intersections of diagonals AC and BD . Four squares of maximum possible area are formed inside each four triangles AOB , BOC , COD and AOD . What is the total area of these 4 squares ? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MENSURATIONBOOK - ARIHANT SSCCHAPTER - MENSURATIONEXERCISE - EXERCISE (LEVEL 2)
68 Videos
- MENSURATIONBOOK - ARIHANT SSCCHAPTER - MENSURATIONEXERCISE - TEST OF YOUR LEARNING
18 Videos
- MENSURATIONBOOK - ARIHANT SSCCHAPTER - MENSURATIONEXERCISE - EXERCISE (MISCELLANEOUS)
59 Videos
- LOGARITHM BOOK - ARIHANT SSCCHAPTER - LOGARITHM EXERCISE - EXERCISE LEVEL 2
19 Videos
- MIXED GRAPHBOOK - ARIHANT SSCCHAPTER - MIXED GRAPHEXERCISE - Higher Skill Level Questions
15 Videos
Similar Questions
Four point masses each mass m kept at the vertices of a square. A point mass m is kept at the point of intersection of the diagonal of a square. What be the force experienced by central mass m ?
View SolutionABCD is a square . Another square EFGH with the same area is placed on the square ABCD such that the point of intersection of diagonals of square ABCD and square EFGH coincide and the sides of square EFGH are parallel to the diagonals of square ABCD. Thus a new figure is formed as shown in the figure . What is the area enclosed by the given figure if each side of the square is 4 cm :

View Solution
Knowledge Check
In the adjoining figure a quadrant ( of circle ) inscribes a square of maximum possible area . If the radius of the circle be 'r' then what is the area of the square ?
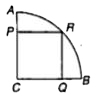 Ar22B3r25Cr2√3D2√6r
Ar22B3r25Cr2√3D2√6rThe point of intersection of diagonals of a square ABCD is at the origin and one of its vertices is at a(4,2). What is the equation of the diagonal BD?
A2x+y=0B2x−y=0Cx+2y=0Dx−2y=0In the adjoining figure a square of maximum possible area is circumscribed by the right angle triangle ABC in such a way that one of its side just lies on the hypotenuse of the triangle . What is the area of the square ?
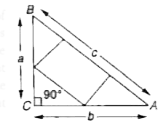 A(abca2+b2+ab)2Ba2+b2+c2abcCabca2+b2+c2Dnone of these
A(abca2+b2+ab)2Ba2+b2+c2abcCabca2+b2+c2Dnone of these
If the length of diagonal BD of a square ABCD is 4.8 cm, the area of the square ABCD is :
View SolutionIf the length of diagonal BD of a square ABCD is 4.8 cm, the area of the square ABCD is :
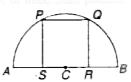
View SolutionIn the adjoining figure PQRS is a square of maximum possible area which is circumscribed by the semicricle . Points R and S lie on the diameter AB. What is the area of the square if the radius of the circle is 'r' ?
View SolutionIn the figure shown square II is formed by joining the mid-points of square II
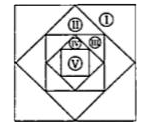
and so on . In this way total five squares are drawn . The sides of the square I is 'a' cm.
What is the total area of all the five squares ?
View SolutionIn the adjoining figure ABC is an equilateral triangle inscribeing a square of maximum possible area . Again in this square there is an equilateral triangle whose side is same as that of the square . Further the smaller equilateral triangle inscribes a square of maximum possible area . What is the area of the innermost square if the each side of the outermost triangle be 0.01 m ?
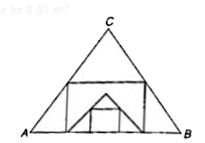
View Solution
