A hemispherical basin 150 cm in diameter holds water one hundred and twenty times as much a cylindrical tube. If the height of the tube is 15 cm , then the diameter of the tube ( in cm ) is :
23
24
25
26
The correct Answer is:C
To solve the problem step by step, we need to find the diameter of a cylindrical tube given that a hemispherical basin holds water that is 120 times the volume of the cylindrical tube.
1. Find the Radius of the Hemispherical Basin:
- The diameter of the hemispherical basin is given as 150 cm.
- The radius r of the hemispherical basin is half of the diameter:
r=1502=75 cm
Hint: Remember that the radius is always half of the diameter.
2. Calculate the Volume of the Hemispherical Basin:
- The formula for the volume V of a hemisphere is:
V=23πr3
- Substituting the radius r=75 cm:
V=23π(75)3
3. Calculate 753:
- First, calculate 753:
753=75×75×75=421875
- Now substitute back into the volume formula:
V=23π(421875)
4. Relate the Volume of the Hemispherical Basin to the Volume of the Cylindrical Tube:
- According to the problem, the volume of the hemispherical basin is 120 times the volume of the cylindrical tube:
Vhemisphere=120×Vcylinder
- The volume V of a cylinder is given by:
Vcylinder=πr2h
- Here, h=15 cm is the height of the cylindrical tube.
5. Set Up the Equation:
- Substitute the volumes into the equation:
23π(421875)=120×πr2(15)
- Cancel π from both sides:
23(421875)=120×r2×15
6. Simplify the Equation:
- Calculate 120×15=1800:
23(421875)=1800r2
- Calculate 23×421875=281250:
281250=1800r2
7. Solve for r2:
- Divide both sides by 1800:
r2=2812501800
- Calculate 2812501800=156.25:
r2=156.25
8. Find the Radius r:
- Take the square root of both sides:
r=√156.25=12.5 cm
9. Calculate the Diameter of the Cylindrical Tube:
- The diameter D is twice the radius:
D=2r=2×12.5=25 cm
Final Answer:
The diameter of the cylindrical tube is 25 cm.
---
- The diameter of the hemispherical basin is given as 150 cm.
- The radius r of the hemispherical basin is half of the diameter:
r=1502=75 cm
- The formula for the volume V of a hemisphere is:
V=23πr3
- Substituting the radius r=75 cm:
V=23π(75)3
- First, calculate 753:
753=75×75×75=421875
- Now substitute back into the volume formula:
V=23π(421875)
- According to the problem, the volume of the hemispherical basin is 120 times the volume of the cylindrical tube:
Vhemisphere=120×Vcylinder
- The volume V of a cylinder is given by:
Vcylinder=πr2h
- Here, h=15 cm is the height of the cylindrical tube.
- Substitute the volumes into the equation:
23π(421875)=120×πr2(15)
- Cancel π from both sides:
23(421875)=120×r2×15
- Calculate 120×15=1800:
23(421875)=1800r2
- Calculate 23×421875=281250:
281250=1800r2
- Divide both sides by 1800:
r2=2812501800
- Calculate 2812501800=156.25:
r2=156.25
- Take the square root of both sides:
r=√156.25=12.5 cm
- The diameter D is twice the radius:
D=2r=2×12.5=25 cm
The diameter of the cylindrical tube is 25 cm.
Topper's Solved these Questions
- MENSURATIONBOOK - ARIHANT SSCCHAPTER - MENSURATIONEXERCISE - EXERCISE (LEVEL 1)
55 Videos
- MENSURATIONBOOK - ARIHANT SSCCHAPTER - MENSURATIONEXERCISE - EXERCISE (LEVEL 2)
68 Videos
- MENSURATIONBOOK - ARIHANT SSCCHAPTER - MENSURATIONEXERCISE - INTRODUCTORY EXERCISE- 10.7
12 Videos
- LOGARITHM BOOK - ARIHANT SSCCHAPTER - LOGARITHM EXERCISE - EXERCISE LEVEL 2
19 Videos
- MIXED GRAPHBOOK - ARIHANT SSCCHAPTER - MIXED GRAPHEXERCISE - Higher Skill Level Questions
15 Videos
Similar Questions
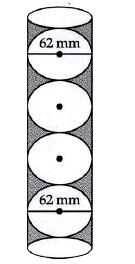
Five tennis balls, diameter 62 mm are placed in cylindrical card tubes. Find the height of the tube :

View SolutionThe difference between inside and outside surfaces of a cylindrical tube 14cm long is 88sq. cm. If the volume of the tube is 176 cubic cm, find the inner and outer radii of the tube.
View Solution
Knowledge Check
A hemispherical basin of 150 cm diameter holds water 120 times as much as a cylindrical tube. If the height of the tube is 15 cm, then the diameter of the tube is
A27 cmB24 cmC25 cmD26 cmIf the end correction of an open tube is 0.3 cm, then the diameter of the tube will be
A1cmB0.3cmC0.5cmD3cmIf the end correction of closed organ pipe is 0.3 cm then the diameter of the tube will be
A0.05mB0.5mC1cmD3cm
A cylindrical tube open at both ends is made of metal. The internal diameter of the tube is 6 cm and length of the tube ie 10 cm. If the thickness of the metal used is 1 cm, then the outer curved surface area of the tube is:
View SolutionFive tennis balls, diameter 62 mm are placed in cylindrical card tubes.Find the volume of the tube :
View SolutionA hollow cylindrical tube open at both end is made of iron 2 cm thick. If the external diameter be 50 cm and the length of the tube is 210 cm, find the number of cubic cm of iron in it.
View SolutionA capillary tube is kept vertical with the lower end dipped in water . The height of water raised in the capillary is 4 cm . If the length of the capillary tube is made 2 cm , then the angle made by the water surface in the capillary with the wall is
View SolutionA cube of metal , whose edge is 10 cm, is wholly immersed in water contained in cylindrical tube whose diameter is 20 cm, by how much will the water level rise in the tube ?
View Solution
