A shopkeeper told me when I have asked him the total number of cellphones in his shop, that he had all Kyocera except three, all Nokia except three, all samsung except three and all L.G. except three. The number of mobile(i.e., cell phones) he had is :
24
256
can't be determined
none of these
The correct Answer is:D
To solve the problem, we need to determine the total number of cellphones in the shop based on the information given by the shopkeeper.
1. Understanding the Information Given:
- The shopkeeper has all Kyocera except three.
- The shopkeeper has all Nokia except three.
- The shopkeeper has all Samsung except three.
- The shopkeeper has all LG except three.
This means that for each brand, there are three cellphones that are not of that brand.
2. Let’s Define the Variables:
- Let K be the number of Kyocera phones.
- Let N be the number of Nokia phones.
- Let S be the number of Samsung phones.
- Let L be the number of LG phones.
- Let T be the total number of phones.
3. Setting Up the Equations:
- From the information given, we can set up the following equations:
- N+S+L=3 (All Kyocera except three)
- K+S+L=3 (All Nokia except three)
- K+N+L=3 (All Samsung except three)
- K+N+S=3 (All LG except three)
4. Adding the Equations:
- If we add all four equations, we get:
(N+S+L)+(K+S+L)+(K+N+L)+(K+N+S)=12
- This simplifies to:
3K+3N+3S+3L=12
- Dividing the entire equation by 3 gives:
K+N+S+L=4
5. Finding the Total Number of Phones:
- The total number of phones T is equal to the sum of all the individual brands:
T=K+N+S+L=4
6. Conclusion:
- Therefore, the total number of cellphones in the shop is T=4.
Final Answer:
The number of mobile phones he had is 4.
- The shopkeeper has all Kyocera except three.
- The shopkeeper has all Nokia except three.
- The shopkeeper has all Samsung except three.
- The shopkeeper has all LG except three.
- Let K be the number of Kyocera phones.
- Let N be the number of Nokia phones.
- Let S be the number of Samsung phones.
- Let L be the number of LG phones.
- Let T be the total number of phones.
- From the information given, we can set up the following equations:
- N+S+L=3 (All Kyocera except three)
- K+S+L=3 (All Nokia except three)
- K+N+L=3 (All Samsung except three)
- K+N+S=3 (All LG except three)
- If we add all four equations, we get:
(N+S+L)+(K+S+L)+(K+N+L)+(K+N+S)=12
- This simplifies to:
3K+3N+3S+3L=12
- Dividing the entire equation by 3 gives:
K+N+S+L=4
- The total number of phones T is equal to the sum of all the individual brands:
T=K+N+S+L=4
- Therefore, the total number of cellphones in the shop is T=4.
The number of mobile phones he had is 4.
Topper's Solved these Questions
- FUNDAMENTALS Book:ARIHANT SSCChapter:FUNDAMENTALS Exercise:TEST OF YOU - LEARNING - 2
Explore 40 Videos
- FUNDAMENTALS Book:ARIHANT SSCChapter:FUNDAMENTALS Exercise:FINAL ROUND
Explore 116 Videos
- FUNCTIONS AND GRAPHBook:ARIHANT SSCChapter:FUNCTIONS AND GRAPHExercise:Final Round
Explore 40 Videos
- GEOMETRYBook:ARIHANT SSCChapter:GEOMETRYExercise:EXERCISE(LEVEL 2)
Explore 52 Videos
Similar Questions
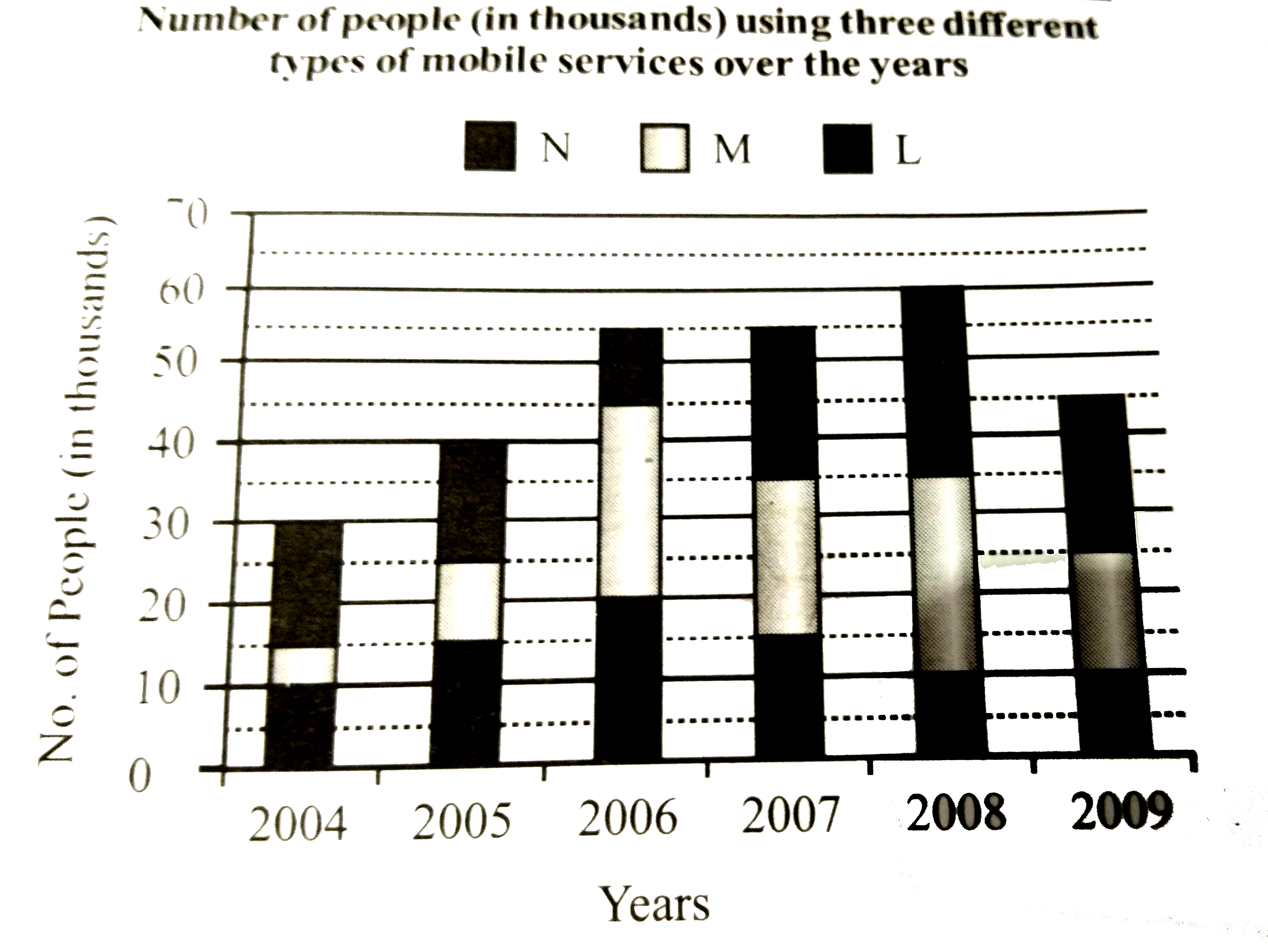
The total number of using all the three mobile services in the year 2004 is what percent of the totoal number of people using all the three mobile services in the year 2008? (rounded off two digits after decimal)
View SolutionIf p, q, r be three positive numbers such that p>q>r when the smallest number is added to the difference of the rest two numbers, then the average of the resultant number and the original numbers except to the smallest is 21 more than the average of all the three numbers. The value of (p-q) is :
View Solution
Knowledge Check
A shopkeeper told me when I have asked him the total number of cellphones in his shop, that he had all Kyocera except three, all Nokia except three, all samsung except three and all L.G. except three. The number of mobile(i.e., cell phones) he had is :
A24B256Ccan't be determinedDnone of theseThe three phases of cellular respiration include all of the following except
AglycolysisBphotosynthesisCKreb's CycleDthe electron transport chainThere are 15 points in a plane, no three of which are in a straight line except 4, all of which are in a straight line. The number of triangles that can be formed by using these 15 points is:
A404B415C451D490
There are n points in a plane no three of which are in the same straight line with the exception of m(n>m)points which are all in the same straight line. Find the number of triangles formed by joining them.
View SolutionI have tied my square bathroom wall with congruent square tiles. All the tiles are red, except those along the two diagonals, which are all blue. If I used 121 blue tiles, then the number of red tiles I used are
View SolutionA man has 3 shirts, 4 trousers and 6 ties. What are the number of ways in which he can dress himself with a combination of all the three?
View SolutionIn the farm - house of Bhuwan Kisan, there were total 14 deer and ducks. One day a thief entered secretely in the farm - house and after killing all the deer and ducks the took away all the stuff except their legs. When Bhuwan noticed it he has found there 38 legs of deer and ducks. The number of deer in the farm house was :
View SolutionWhich of the following are the basic components present in connective tissue except blood ?
View Solution
