I have tied my square bathroom wall with congruent square tiles. All the tiles are red, except those along the two diagonals, which are all blue. If I used 121 blue tiles, then the number of red tiles I used are
900
1800
3600
7200
The correct Answer is:A
(a) Let the square has dimensions n×n.
If n is even, total no. of blue (diagonal) tiles =n+n=2n
If n is odd, then total no. of blue tiles =n+n−1=2n−1
(the middle tile is be counted twice).
Hence, 2n−1=121⇒n=61
So, number of red tiles =61×61−121=3600
Topper's Solved these Questions
- PERMUTATION AND COMBINATIONBOOK - CENGAGECHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Multiple Correct Answer
2 Videos
- PERMUTATION AND COMBINATIONBOOK - CENGAGECHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Comprehension
8 Videos
- PARABOLABOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Question Bank
21 Videos
- PRINCIPLE OF MATHEMATICAL INDUCTIONBOOK - CENGAGECHAPTER - PRINCIPLE OF MATHEMATICAL INDUCTIONEXERCISE - Exercise
9 Videos
Similar Questions
A rectangular path of 60m length and 3m width is covered by square tiles of side 25cm. How many tiles will there be in one row along its width? How many such rows will be there? Find the number of tiles used to make this path?
View SolutionA rectangular path of 60 m length and 3 m width is covered by square tiles of side 25 cm. How many tiles will there be in one row along its width? How many such rows will be there? Find the number of tiles used to make this path?
View Solution
Knowledge Check
It was time for celebrations in the Gryffindor common room. But as luck would have had it, Seamus miscued a spell setting the common room floor on fire. The students were evacuated quickly. Dumbledore was informed of this act and he thought of the perfect punishment for Seamus. He had to tile the common room without using magic (of course). The room was two units wide and N units long. Seamus was provided with two types of tiles: a rectangle that is one unit wide and two units long, and a L-shaped tile covering 3 square units. Pictures of the tiles are shown below. Seamus was allowed to rotate the tiles as he laid them. He had an unlimited supply of tiles. He however failed, and requested Harry to help. Harry said that he could only tell the number of different ways of tiling the room using these tiles. For instant, a2×3 room could be tiled in 5 different ways as follows:

Notice that the tiling could use both types of tiles. consider the tiling of a2×4 room below.
Seamus then asks Harry for the number of different ways of tiling a room of dimension 2×12. What would be Harry's answer?A1055B1255C1455D1450Swimming further, he could feel something sucking the water out of the sea. He saw a huge 6ft×6ft hole dug, which was pulling all the water. He has to fill it with some 2×2 square tiles and some 4×1 rectangular tiles. After arranging the tiles to cover the lava perfectly without overlap, excess pressure caused one of the tiles to smash. Unfortunately, the only spare tile is of the other shape to the one smashed. Will Mario be able to rear- range the remaining unsmashed tiles to perfectly cover the hole again?
AYesBNoCYes,Only if broken tile is 4×1DYes,Only if broken tile is 2×2
The length and breadth of the floor of the room are 20 feet and 10 feet respectively. Square tiles of 2 feet length of different colours are to be laid on the floor. Black tiles are laid in the first row on all sides. If white tiles are laid in the one-third of the remaining and blue tiles in the rest, how many blue tiles will be there? (a) 16 (b) 24 (c) 32 (d) 48 (e) None of these
View SolutionA rectangular courtyard is 3m 78 cm long and 5m 25 cm broad. It is desired to prove it with square tiles of the same size. What is the largest size of the tile that can be used ? Also find the number of such tiles.
View SolutionI have 3 normal dice, one red. one blue and one green and I roll all three simultaneously. Let P be the probability that the sum of the numbers on the red and blue dice is equal to the number on the green die. If P is the written in lowest terms as a/b then the value of (a+b) equals -
View SolutionA rectangular courtyard, 3.78 m long and 5.25 m broad, is to be paved exactly with square tiles, all of the same size. Find the least number of square tiles covered.
View SolutionSonal and Anmol made a sequence of tile designs from square white tiles surrounding one square purple tile. The purple tiles come in many sizes. Three of the designs are shown below.
(a) Copy and complete the table
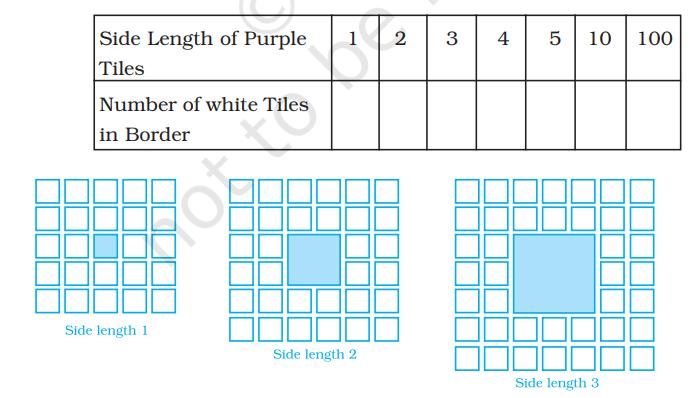
(b) Draw a graph using the first five pairs of numbers in your table.
(c) Do the points lie on a line?
View SolutionA child's game has 8 triangle of which 3 are blue and rest are red, and 10 square of which 6 are blue and rest are red. One piece is lost at random. Find the probability that it is a
(i) trinagle (ii) square
(iii) square of blue colour
(iv) triangle of red colour
View Solution
