The expression
where n = 100, then value of N is:
9900
none of these
The correct Answer is:A
To solve the expression
N=11+1×1+12+2×2+13+3×3+14+4×4+…+1n+n×n
where n=100, we can simplify each term in the series.
Step 1: Simplify each term
Each term in the series can be expressed as:
1k+k×k=1k+k2=1k(1+k)
Thus, we can rewrite N as:
N=100∑k=11k(1+k)
Step 2: Decompose the fraction
We can use partial fraction decomposition on the term 1k(1+k):
1k(1+k)=1k−11+k
Step 3: Rewrite the sum
Now substituting back into the sum, we have:
N=100∑k=1(1k−11+k)
Step 4: Expand the sum
This can be expanded as:
N=(11−12)+(12−13)+(13−14)+…+(1100−1101)
Step 5: Notice the cancellation
In this series, most terms will cancel out:
N=1−1101
Step 6: Calculate the final value
Thus, we can simplify this to:
N=1−1101=101101−1101=100101
Final Answer
So, the value of N is:
N=100101
---
Topper's Solved these Questions
- FUNDAMENTALS Book:ARIHANT SSCChapter:FUNDAMENTALS Exercise:TEST OF YOU - LEARNING - 2
Explore 40 Videos
- FUNDAMENTALS Book:ARIHANT SSCChapter:FUNDAMENTALS Exercise:FINAL ROUND
Explore 116 Videos
- FUNCTIONS AND GRAPHBook:ARIHANT SSCChapter:FUNCTIONS AND GRAPHExercise:Final Round
Explore 40 Videos
- GEOMETRYBook:ARIHANT SSCChapter:GEOMETRYExercise:EXERCISE(LEVEL 2)
Explore 52 Videos
Similar Questions
Knowledge Check
If 16n+1=64×4−n, the value of n is
A13B19C12D1If P(n) is the statement ,
''11×2+12×3+12×3+13×4+…..+1n(n+1)=nn+1' then P(n) is true forAn>2Bn∈ZCn∈NDNo value of nIf n!,3×(n!) and (n+1)! are in GP, then the value of n will be
A3B4C8D10
Find the sum 1×2×.nC1+2×3×.nC2+…..+2×(n+1)×.nCn.
View SolutionIf 1×2×3×…….×n is denoted by
 , then
, then 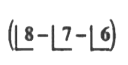 is equal to :
is equal to :
View SolutionThe statement P(n): ''1×1!+2×2!+3×3!+...+n×Xn!=(n+1)!−1''is
View SolutionIf (1×2×3×4×....×n!) = n, then (14! - 13! - 12!) is equal to
View SolutionSimplify: 16×2n+1−4×2n16×2n+1−2×2n+2.
View Solution