Question

Let ABC be an equilateral triangle inscribed in the circle $x^2+y^2=a^2$ . Suppose pendiculars from A, B, C to the ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1,(a>b)$ meets the ellipse respectivelily at P, Q, R so that P, Q , R lies on same side of major axis as A, B, C respectively. Prove that the normals to the ellipse drawn at the points P Q nad R are concurrent.

Explanation

Let the coordinates of a A= ( a cos , sin theta ) , that the corrdinates of

`B= { alpha ( theta + 2 pi //3) , a sin theta + 2 pi /3 )}`
`and C= { alpha ( theta + 4 pi //3) , alpha sin ( theta + 4 pi //3 ) }`
according to the given condition , coordition coordinate of P are `( a cos theta b sin theta )` and that of Q are `( alpha cos ) theta+ 2pi //3).`
`b sin ( theta 2pi //3) and ` that of R are
`alpha cos ( theta + 4pi//3) , b sin ( theta + 4 pi //3)`

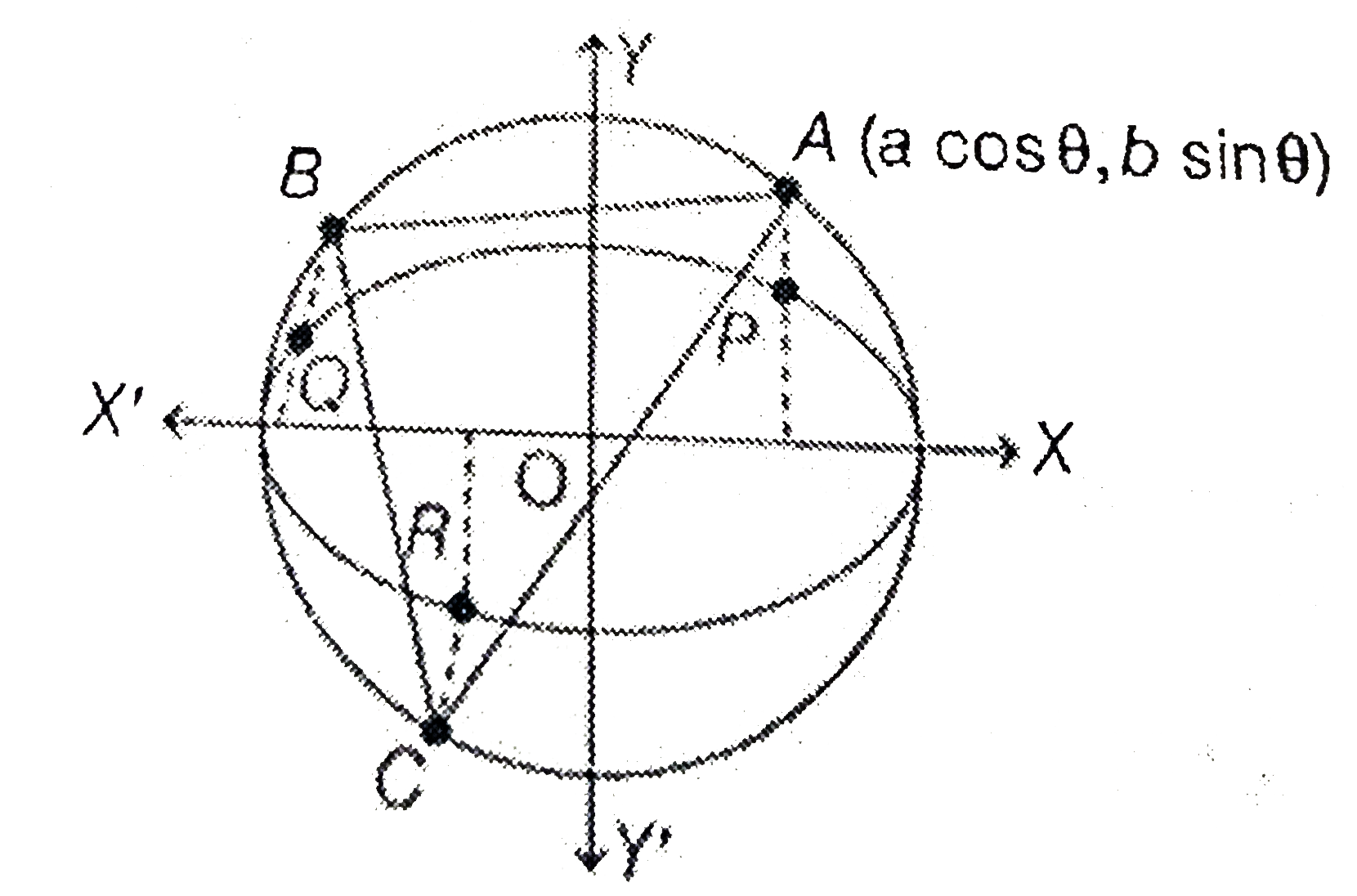
`[:' ` it is given normal that P,Q,R are on the same side of X-axis as A,B and C]
Equataion of the normal to the ellipse at Q is
`( ax)/( cos theta) -( by ) /( sin theta)= a^(2)-b^(2)`
`or ax sin theta - by cos ( theta +(2pi)/(3))`
`=(1)/(2) (a^(2) - b^(2)) sin ( 2 theta + ( 4pi )/(3))`
Equation of normal to the ellipse at R is
`a x sin ( theta + 4pi/3) - by cos( theta + 4pi//3) `
` =(1)/(2) (a^(2)- b^(2)) sin ( 2 theta + 8 pi //3) `
but ` sin ( theta + 4pi//3)= sin ( 2pi + theta - 2pi//3)`
`=sin ( theta - 2pi //3)`
`and cos ( theta + 4pi//3)= cos ( 2pi + theta //3)`
` = cos ( theta - 2pi +2 pi //3)`
`and sin ( 2 theta + 8 pi //3 )= sin ( 4 pi+ 2 theta -4pi //3)`
`= sin ( 2 theta - 4pi //3)`
Now ,Eq .(iii) can be written as ax sin `( theta - 2pi //3)- by cos ( theta - 2pi//3)`
`=(1)/(2)(a^(2)-b^(2))sin ( 2 theta - 4pi//3) `
for the lines (i) , (ii) and (iv) to be concurrent , we must have the determinant
`Delta_(1)=|{:(a sin theta, - b sin theta, (1)/(2)(a^(2)-b^(2))sin 2 theta),(a sin (theta+(2pi)/(3)), -b cos (0+(2pi)/(3)),(1)/(2)(a^(2)-b^(2)) sin ( 2theta + 4 pi//3)),(a sin ( theta-( 2pi)/(3)),- b cos(theta-(2pi)/(3)), (1)/(2)(a^(2)- b^(2))sin (2 theta- 4pi//3)):}|=0`
thus , lines (i) ,(ii) and (iv) are consurrent.