The line passing through the extremity $A$ of the major exis and extremity $B$ of the minor axis of the ellipse $x^{2} + 9 y^{2} = 9$ meets is auxiliary circle at the point $M .$ Then the area of the triangle with vertices at $A, M,$ and $O$ (the origin) is 31/10 (b) 29/10 (c) 21/10 (d) 27/10

A

$\frac{31}{10}$

B

$\frac{29}{10}$

C

$\frac{21}{10}$

D

$\frac{27}{10}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Equations of auxilary circle is
$x^{2} + y^{2} = 9$
Euations of AM is $\frac{x}{3} + \frac{y}{1} = 1$

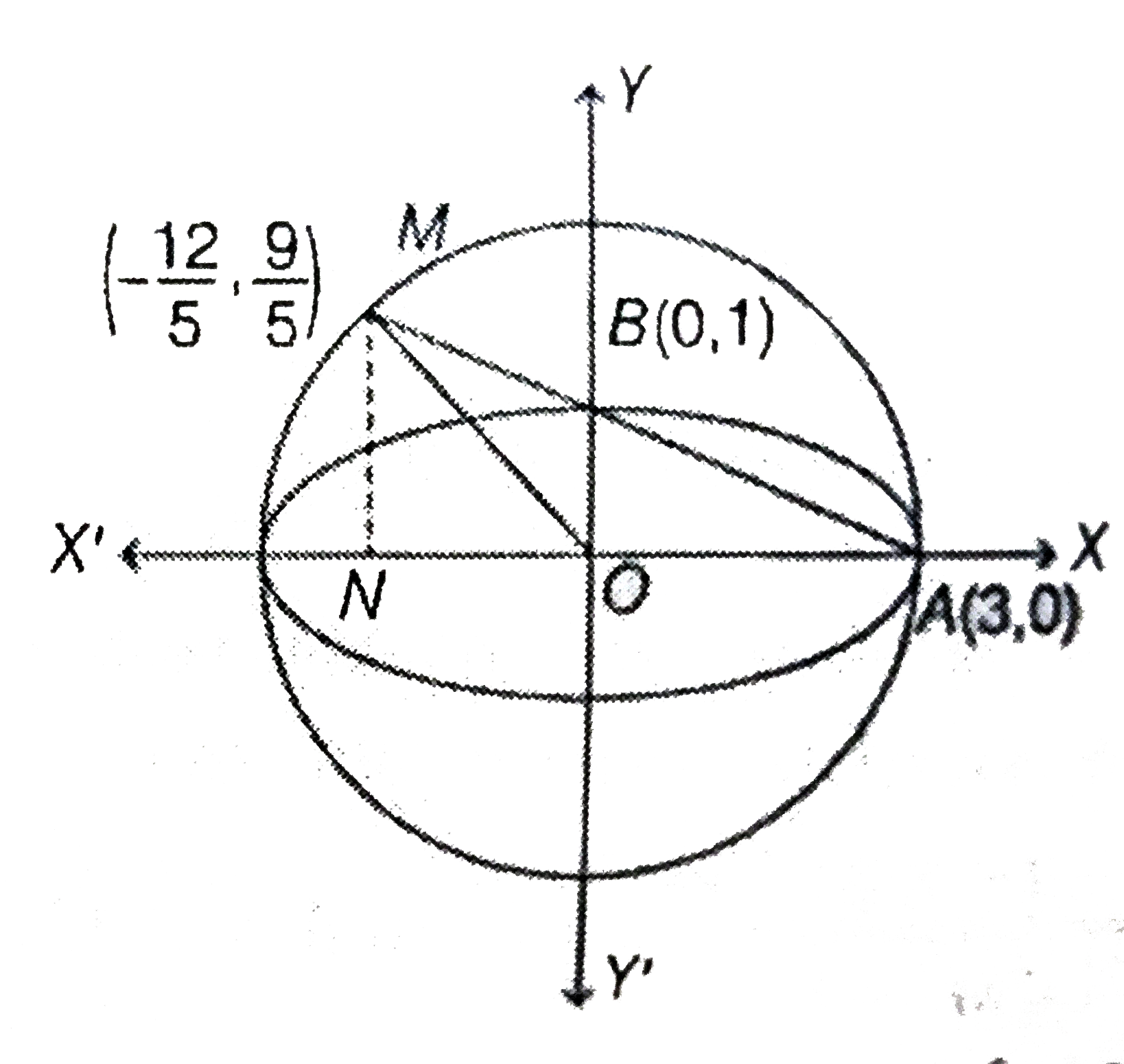
On solving Eqs.(i) and (ii) we get M $(- \frac{12}{5}, (9), (5))$
Now , area of $Δ A P O M = \frac{1}{2} O A \times M N = \frac{27}{10}$ sq units.

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The line passing through the extremity $A$ of the major exis and extremity $B$ of the minor axis of the ellipse $x^{2} + 9 y^{2} = 9$ meets is auxiliary circle at the point $M .$ Then the area of the triangle with vertices at $A, M,$ and $O$ (the origin) is 31/10 (b) 29/10 (c) 21/10 (d) 27/10
A $\frac{31}{10}$
B $\frac{29}{10}$
C $\frac{21}{10}$
D $\frac{27}{10}$
Question 2 - Select One
The line passing through the extremity $A$ of the major exis and extremity $B$ of the minor axis of the ellipse $x^{2} + 9 y^{2} = 9$ meets is auxiliary circle at the point $M .$ Then the area of the triangle with vertices at $A, M,$ and $O$ (the origin) is 31/10 (b) 29/10 (c) 21/10 (d) 27/10
A $31 / 10$
B $29 / 10$
C $21 / 10$
D $27 / 10$
Question 3 - Select One
The line passing through the extremity A of the major axis and extremity B of the minor axis of the elliopse $x^{2} + 9 y^{2} = 9$ , meets the auxillary circle at the point M, then the area of the triangle with vertices at A,M and the origin O is N
A $31 / 10$
B $29 / 10$
C $21 / 10$
D $27 / 10$

IIT JEE PREVIOUS YEAR-ELLIPSE-EQUATION OF TANGENT AND NORMAL

Home
Ask Doubt
Profile