The area (in sq. units) of the quadrilateral formed by the tangents at the end points of the latera recta to the ellipse $\frac{x^{2}}{9} + \frac{y^{2}}{5} = 1$ , is: (1) $\frac{27}{4}$ (2) 18 (3) $\frac{27}{2}$ (4) 27

A

$\frac{27}{4}$

B

18

C

$\frac{27}{2}$

D

27

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

given equation of ellipse is
$\frac{x^{2}}{9} + \frac{y^{2}}{5} = 1$
$∴ a^{2} = 9, b^{2} = 5 \Rightarrow a = 3, b = \sqrt{5}$
Now, $e = \sqrt{1 + \frac{b^{2}}{a^{2}}} = \sqrt{1 - \frac{5}{9}} = \frac{2}{3}$
FOci $= (\pm a e, 0) = (\pm 2, 0) and \frac{b^{2}}{a} = \frac{5}{3}$

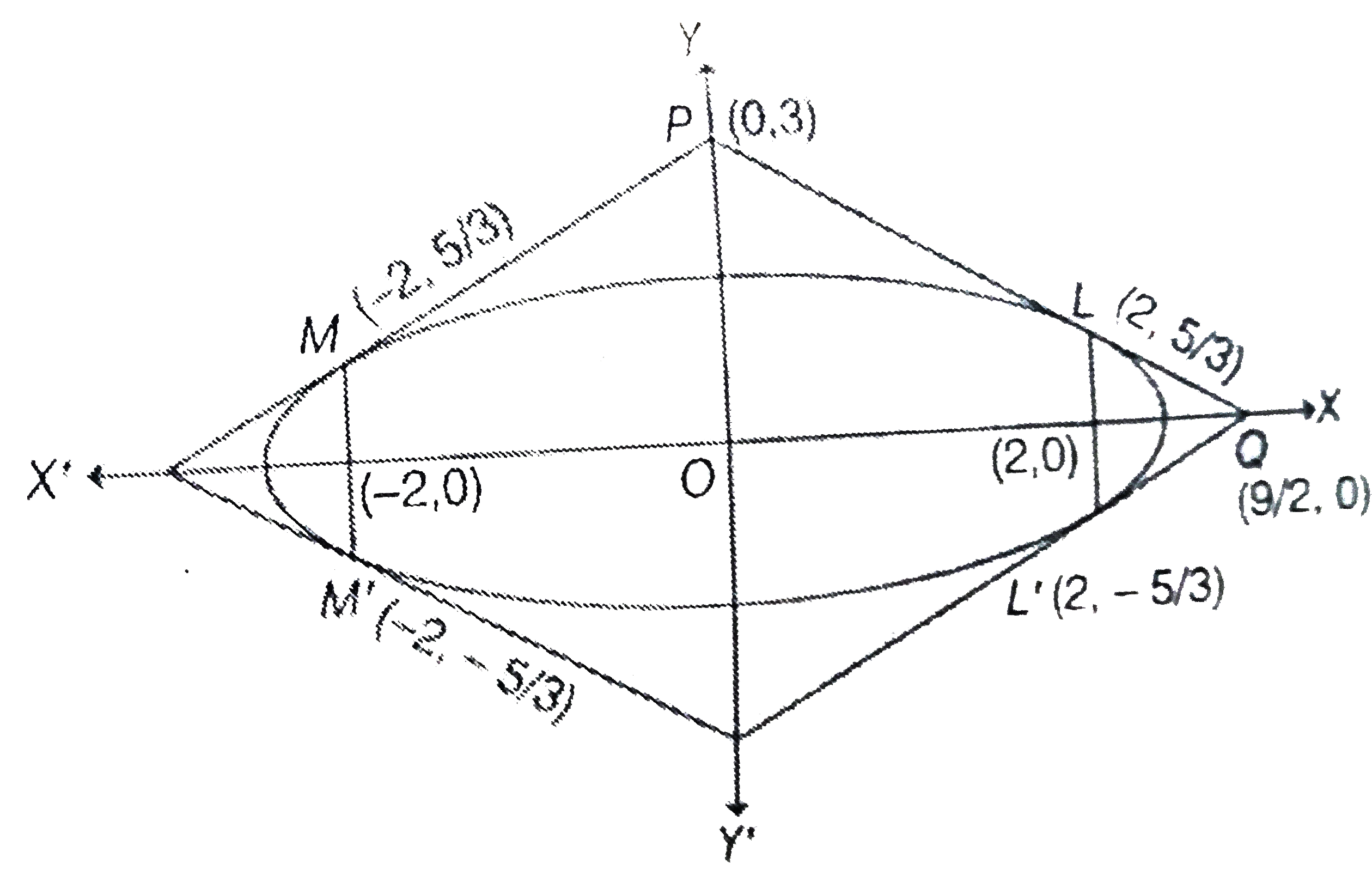
$∴$ Extremities of one of latusrectum are
$(2, \frac{5}{3}) and (2, \frac{- 5}{3})$
$∴$ Equation of tangent at $(a, \frac{5}{3})$ is
$\frac{x (2)}{9} + \frac{y (5 / 3)}{5} = 1 or 2 x + 3 y = 9$
since Eq. (ii) intersects X and Y - axes at $(\frac{9}{2}, 0)$ and (0,3) ., respectively .
$∴$ Area of qudarlateral $= 4 \times$ Area of $Δ P O Q$
$= 4 \times (\frac{1}{2} \times \frac{9}{2} \times 3) = 27$ sq units

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The area of the quadrilateral formed by the tangents at the end points of latus rectum of the ellipse $5 x^{2} + 9 y^{2} = 45$ is
A9
B27/2
C27/4
DNone of these
Question 2 - Select One
Area (in sq. units) of the triangle formed by the lines $x^{2} + 4 x y + y^{2} = 0 and x + y = 1$ is
A $\sqrt{3}$
B2
C1
D $\frac{\sqrt{3}}{2}$
Question 3 - Select One
The area (in sq. units) bounded by the parabola $y = x^{2} - 1$ , the tangent at the point (2,3) to it and the y-axis is
A $\frac{14}{3}$
B $\frac{56}{3}$
C $\frac{8}{3}$
D $\frac{32}{3}$

IIT JEE PREVIOUS YEAR-ELLIPSE-EQUATION OF TANGENT AND NORMAL

Home
Ask Doubt
Profile