All ………………. Triangles are similar. (isoceles, equilaterial)
The correct Answer is:equilaterial
To solve the question "All ………………. Triangles are similar. (isosceles, equilateral)", we need to analyze the properties of isosceles and equilateral triangles.
1. Understanding Triangle Types:
- An isosceles triangle has at least two sides that are equal in length and the angles opposite those sides are equal.
- An equilateral triangle has all three sides equal in length and all three angles equal (each measuring 60 degrees).
2. Identifying Similarity:
- Two triangles are said to be similar if their corresponding angles are equal and the lengths of their corresponding sides are in proportion.
3. Analyzing Isosceles Triangles:
- In isosceles triangles, while two sides are equal, the third side can vary in length. This means that isosceles triangles can have different shapes and sizes, leading to different angles.
- Therefore, isosceles triangles are not necessarily similar to each other unless they have the same angles.
4. Analyzing Equilateral Triangles:
- All equilateral triangles have equal sides and equal angles (60 degrees each). This means that any equilateral triangle can be transformed into another equilateral triangle by scaling (enlarging or reducing) without changing the shape.
- Thus, all equilateral triangles are similar to each other.
5. Conclusion:
- Since all equilateral triangles maintain the same angle measures and side ratios, we can conclude that:
- All equilateral triangles are similar.
Final Answer:
All equilateral triangles are similar.
---
- An isosceles triangle has at least two sides that are equal in length and the angles opposite those sides are equal.
- An equilateral triangle has all three sides equal in length and all three angles equal (each measuring 60 degrees).
- Two triangles are said to be similar if their corresponding angles are equal and the lengths of their corresponding sides are in proportion.
- In isosceles triangles, while two sides are equal, the third side can vary in length. This means that isosceles triangles can have different shapes and sizes, leading to different angles.
- Therefore, isosceles triangles are not necessarily similar to each other unless they have the same angles.
- All equilateral triangles have equal sides and equal angles (60 degrees each). This means that any equilateral triangle can be transformed into another equilateral triangle by scaling (enlarging or reducing) without changing the shape.
- Thus, all equilateral triangles are similar to each other.
- Since all equilateral triangles maintain the same angle measures and side ratios, we can conclude that:
- All equilateral triangles are similar.
All equilateral triangles are similar.
Topper's Solved these Questions
- TRIANGLESBook:MBD -HARYANA BOARDChapter:TRIANGLESExercise:SHORT ANSWER TYPES QUESTIONS
Explore 9 Videos
- TRIANGLESBook:MBD -HARYANA BOARDChapter:TRIANGLESExercise:SHORT ANSWER TYPES QUESTIONS
Explore 9 Videos
- SURFACE AREAS AND VOLUMESBook:MBD -HARYANA BOARDChapter:SURFACE AREAS AND VOLUMESExercise:LONG ANSWER TYPE QUESTIONS
Explore 16 Videos
Similar Questions
Fill in the blanks using the correct word given in brackets: All circles are ......... (congruent, similar) All squares are ....... (similar, congruent) (iii) All ...... triangles are similar (isosceles, equilaterals):
View SolutionFill in the blank using the correct word given in bracket.
All ...............triangles are similar. (Isosceles/Equilateral)
View SolutionWhich of the following is/ are true ?
(a) All triangles are similar.
(b) All circles are similar.
(c) All squares are similar.
View SolutionTwo triangle are called similar if
View SolutionIn each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form.
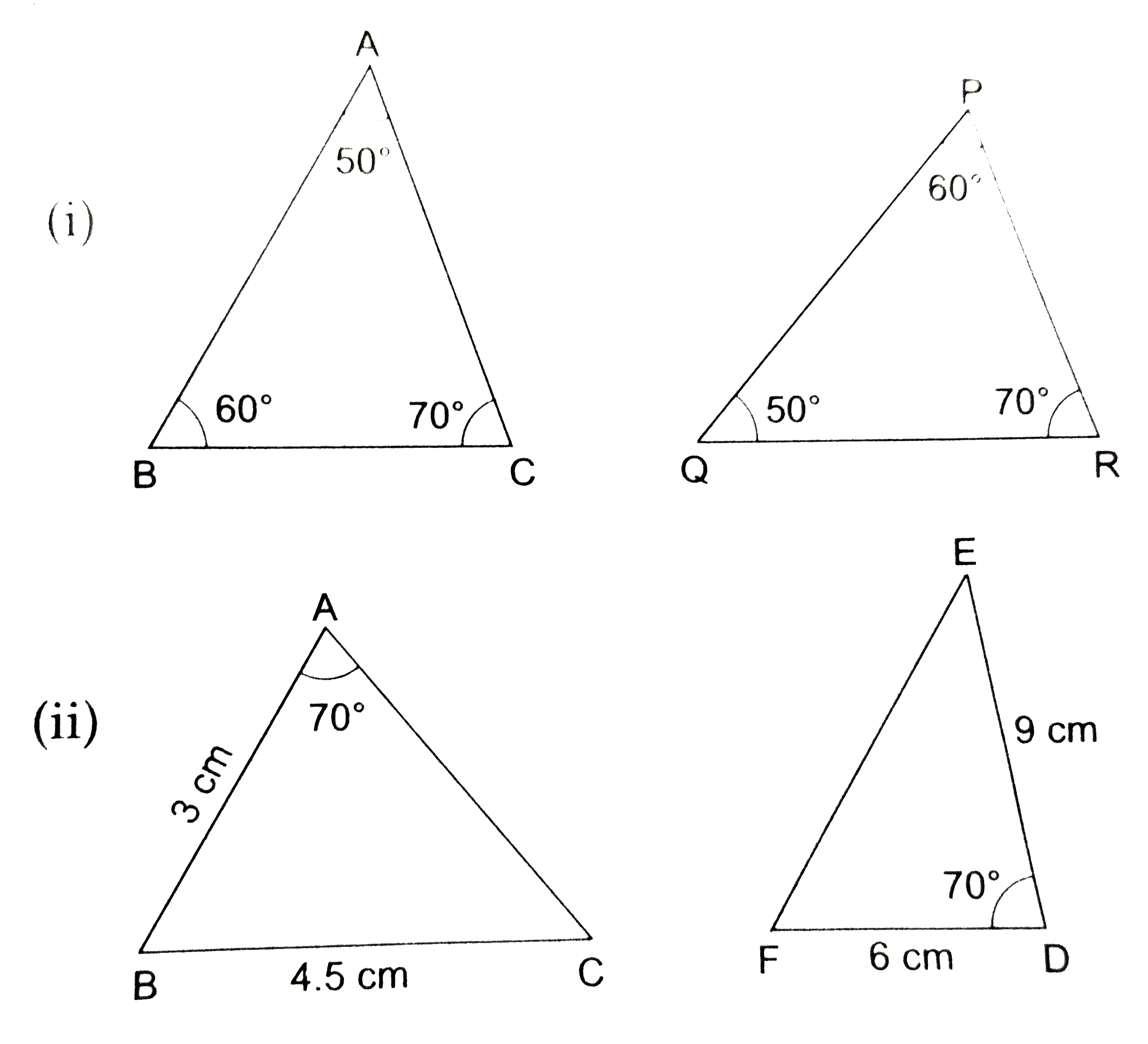
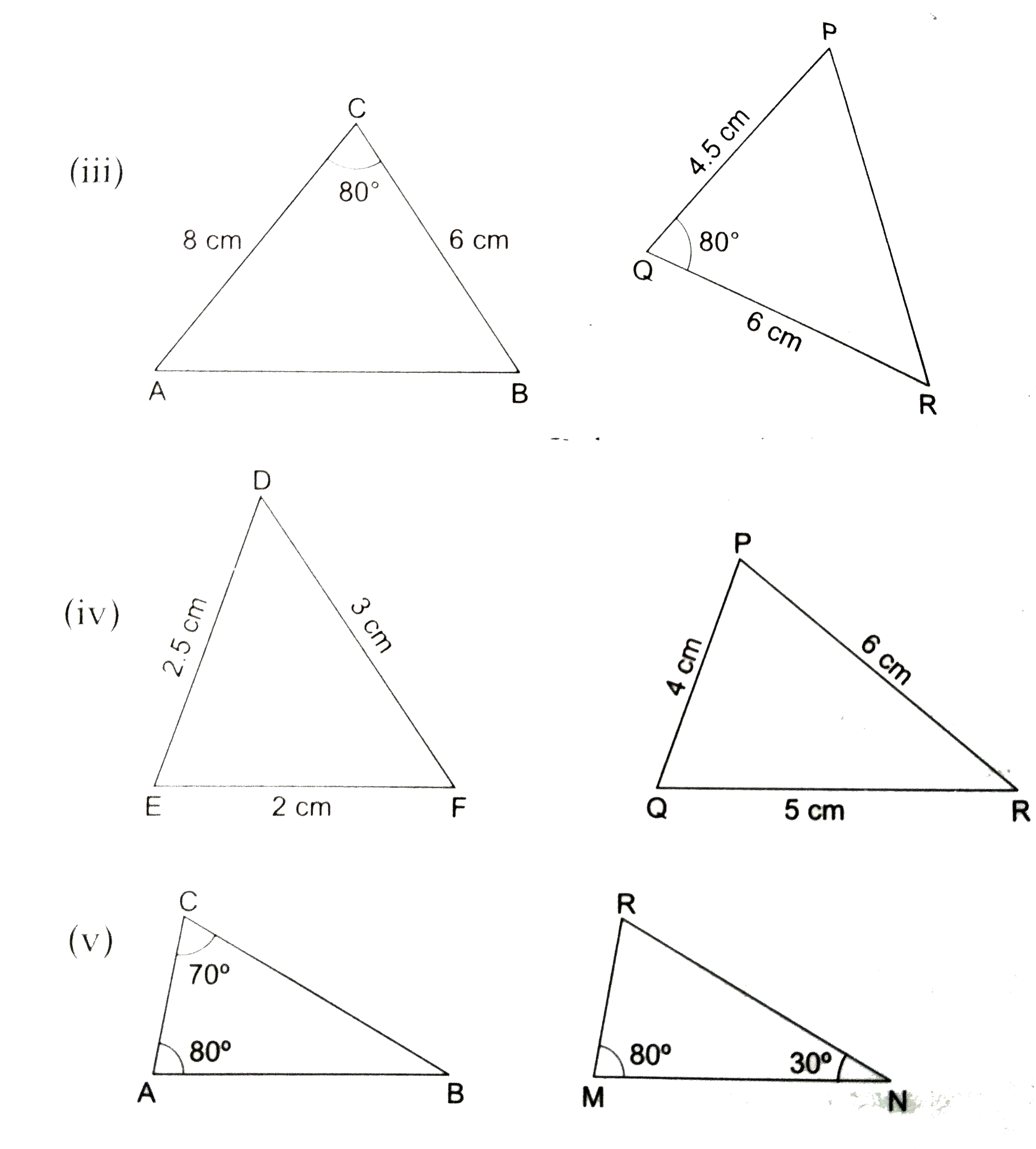
View SolutionA triangle is formed by joining the mid- points of the sides of a given triangle. This process is continued indefinitely. All such triangles formd are similar to one another. (True/False).
View SolutionState which pairs of triangles in Figure are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form:
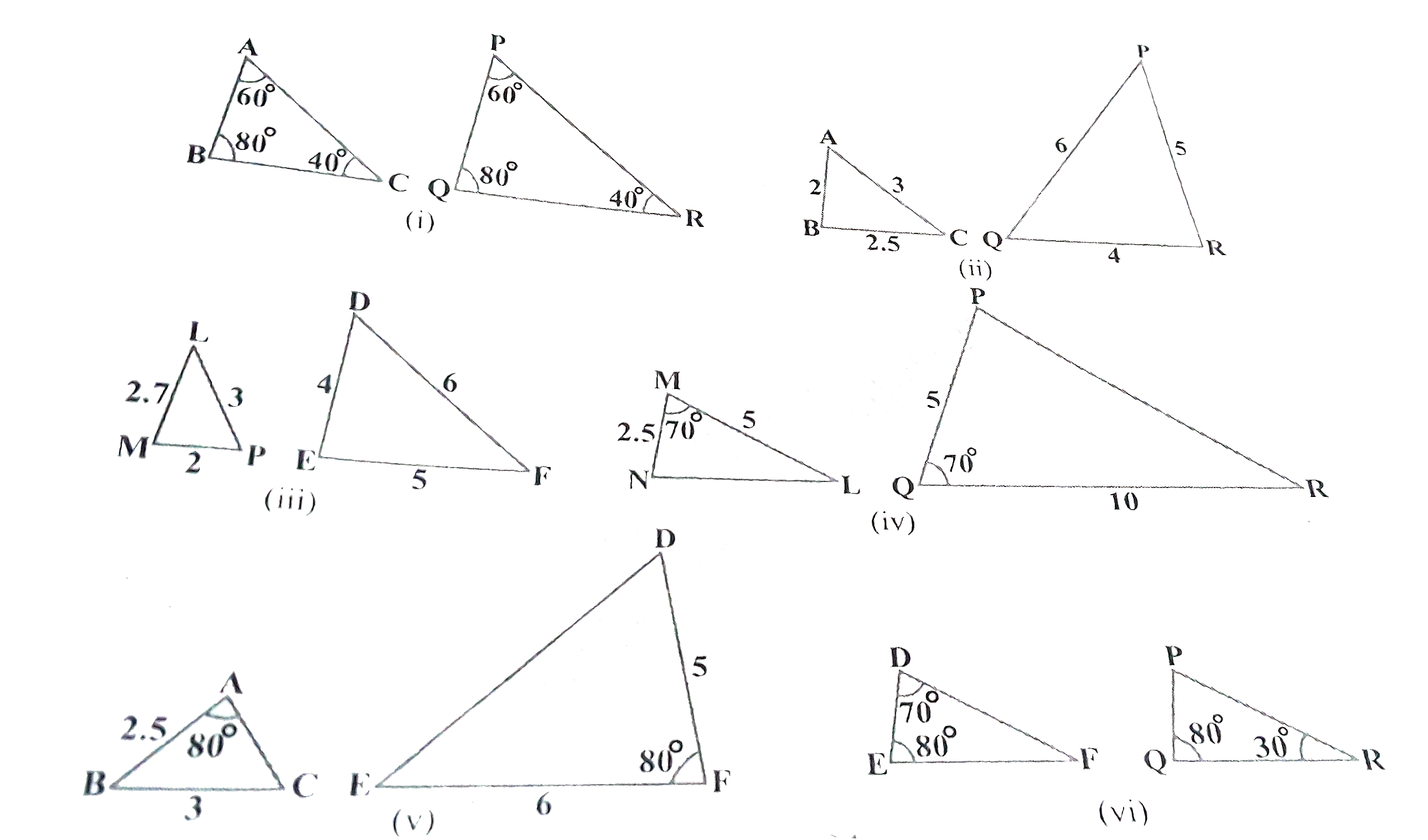
View SolutionSimilar Triangles and their properties
View SolutionAll squares are ……………… . (congruent, similar)
View SolutionO is a point in the interior of a square ABCD such that ΔOAB is an equilateral triangle . Show that ΔOCD is an isoceles triangle .
View Solution

