Two triangle are called similar if
No angles of two triangles are equal
One angle and one side is equal to another triangle angle and side
The two angles of one triangle are equal to the two anges of the other triangle
No sides are equal
To determine when two triangles are called similar, we can follow these steps:
1. Understanding Similarity:
- Two triangles are considered similar if they have the same shape, which means their corresponding angles are equal, and their corresponding sides are in proportion.
2. Identifying Corresponding Angles:
- For two triangles to be similar, we need to check the angles. If the angles of one triangle are equal to the angles of another triangle, they are similar.
3. Checking Proportional Sides:
- In addition to having equal angles, the sides of the triangles must also be in proportion. This means that the ratio of the lengths of corresponding sides must be the same.
4. Using Angle-Angle (AA) Criterion:
- A common criterion for triangle similarity is the Angle-Angle (AA) criterion. If two angles of one triangle are equal to two angles of another triangle, then the triangles are similar.
5. Conclusion:
- Therefore, two triangles are called similar if their corresponding angles are equal (or if two angles of one triangle are equal to two angles of the other triangle).
Final Answer:
Two triangles are called similar if two angles of one triangle are equal to two angles of the other triangle.
- Two triangles are considered similar if they have the same shape, which means their corresponding angles are equal, and their corresponding sides are in proportion.
- For two triangles to be similar, we need to check the angles. If the angles of one triangle are equal to the angles of another triangle, they are similar.
- In addition to having equal angles, the sides of the triangles must also be in proportion. This means that the ratio of the lengths of corresponding sides must be the same.
- A common criterion for triangle similarity is the Angle-Angle (AA) criterion. If two angles of one triangle are equal to two angles of another triangle, then the triangles are similar.
- Therefore, two triangles are called similar if their corresponding angles are equal (or if two angles of one triangle are equal to two angles of the other triangle).
Two triangles are called similar if two angles of one triangle are equal to two angles of the other triangle.
Similar Questions
Two triangles are similar if their corresponding sides are ………….
View SolutionWrite the truth value (T/F) of each of the following statements: (1)Two polygons are similar if their corresponding angles are proportional. (2)Two triangles are similar if their corresponding sides are proportional. (3) Two triangles are similar if their corresponding angles are proportional.
View Solution
Knowledge Check
If in two triangles ABC and PQR, ABPQ=BCRP, then for the two triangles to be similar, which of the following condition is necessary?
A∠B=∠QB∠A=∠PC∠B=∠PD∠A=∠QIf in triangles ABC and PQR, ABPQ=BCRP then write the equality of angles of the two triangles such that two triangles are similar.
A∠A=∠B∠B=∠PC∠C=∠QD∠B=∠Q
If in two right triangles, one of the acute angles of one triangle is equal to an acute angle of the other triangle. Can you say that two triangles will be similar? Why?
View SolutionIn the adjoining figure, ∠ABC=75∘,∠EDC=75∘. State which two triangle are similar and by which test? Also write the similarity of these two triangles by a proper one to one correspondence.
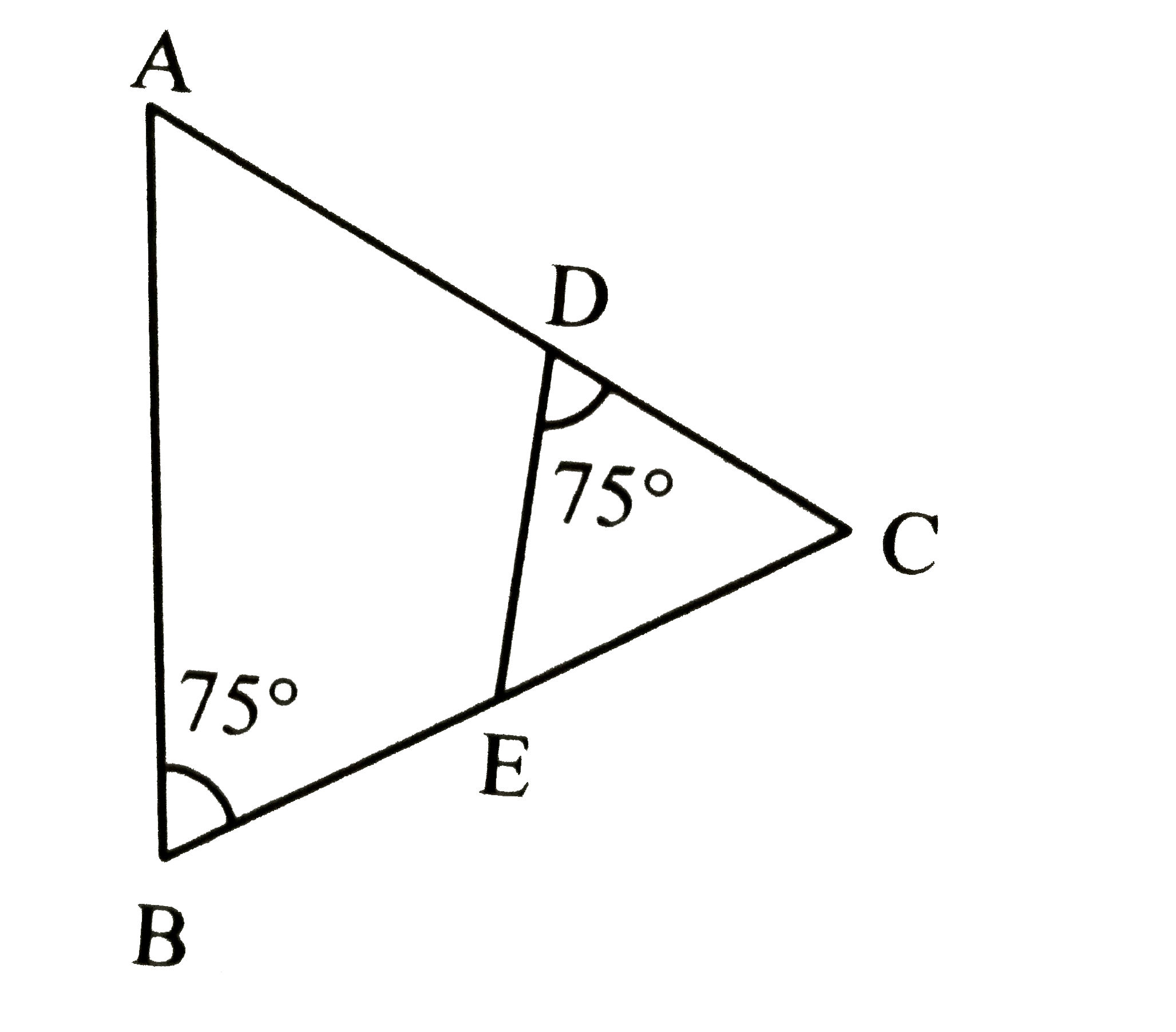
View SolutionIn the figure ∠ABC=75∘
∠EDC=75∘
State which two triangles are similar and by which test? Also
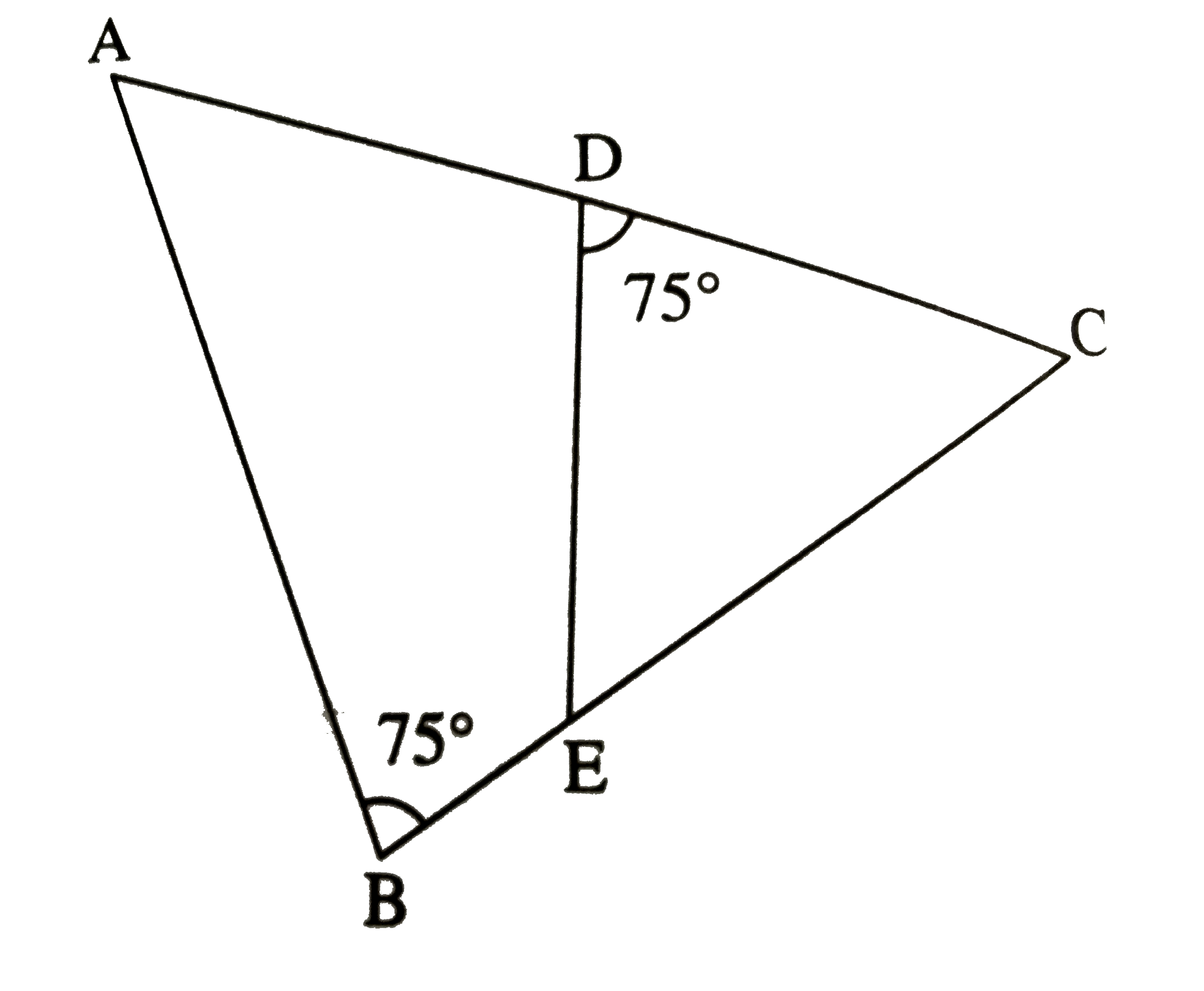
write the similarity of these two triangles by a proper one to one correspondence.
View SolutionSAS Similarity Criterion : If in two triangle; one pair of corresponding sides are proportional and the included angles are equal then two triangles are similar.
View SolutionIf two angles of one triangle are respectively equal to two angles of another triangle; then two triangles are similar.
View SolutionIf in triangles ABC and PQR, ABPQ=ACRP then write the equality of angles triangles of the two triangles such that two triangles are similar.
View Solution
