A fine pencil of $β$ -particles, moving with a speed v, enters a region (region I), where a uniform electric field and a uniform magnetic field are both present. These $β$ -particles then move into region II where only the magnetic field, (out of the two fields present in region I) exists. The path of the $β$ -particles, in the two regions is as shown in the figure.

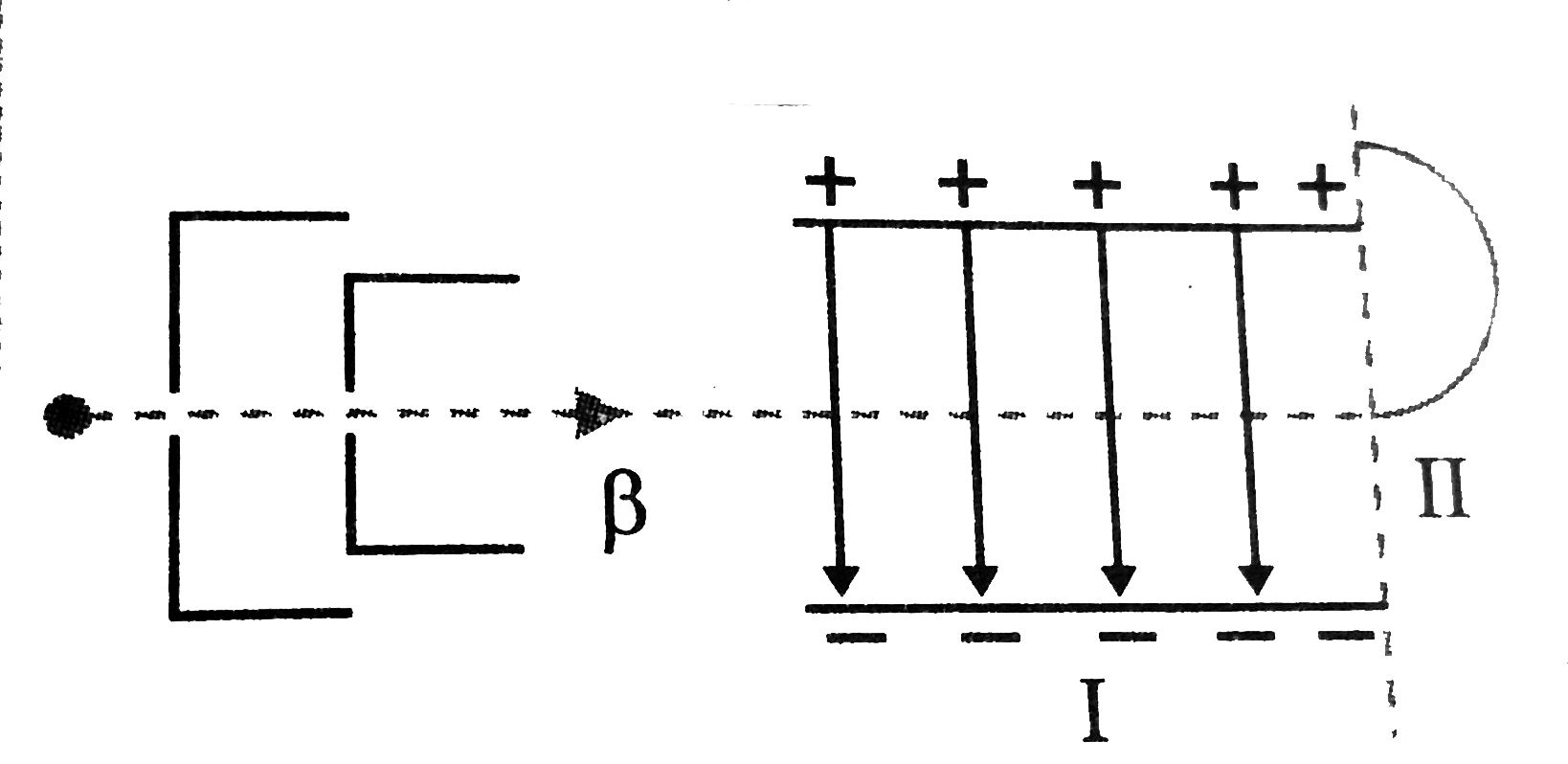
(i) state the direction of magnetic field.
(ii) state the relation between E and B in region I.
(iii) Drive the expression for the radius of the circular path of the $β$ -particle in region II.
(iv) If the magnitude of magnetic field, in region II is changed to n times its earlier value, (without changing the magnetic field in region I) find the factor by which the radius of this circular path would change.

Video Solution

Text Solution

Verified by Experts

(i) The $β$ - particle is passing through both electric and magnetic fields and suffers no deviation i.e., it goes straight through region I where both $\to E and \to B$ are present. It means that the force on $β$ particle due to electric field $(- e \to E)$ , acting upwards is equal and opposite to the force due to magnetic field which is $- e (\to v \times \to B)$ , acting downwards.
Using Fleming.s left hand rule, the direction of magnetic field $(\to B)$ is perpendicular to the plane of paper and inward.
(ii) Force due to electric field = Force due to magnetic field
$e E = e v B {sin 90}^{\circ}$
$e E = e v B$
$v = \frac{E}{B}$
(iii) Let r be the radius of circular path of $β$ particle in region II.
Then $e v B = \frac{m v^{2}}{r}$
$r = \frac{m v}{e B}$
If magnetic field is maden times i.e.
$B . = n B$
The new radius , $r . = \frac{m v}{e n B} = \frac{1}{n} \frac{m v}{e B}$
$\Rightarrow r . = \frac{1}{n} r$

Updated on:21/07/2023

In a region where both non-zero uniform electric field and magnetic field coexist, the path of a charged particle
Acan not be a circle
Bmay be a circle
Cmay be a straight line
Dmay be a helix
A charge particle travels along a straight line with a speed v in region where both electric field E and magnetic field b are present.It follows that
A $| E | = | B |$ and the two field are perpendicular
B $| E | = v | B |$ and the two field are perpendicular
C $| B | = v | E |$ and the two field are parallel
D $| B | = v | E |$ and the two fields are perpendicular
A charged particle is released from rest in a region of steady uniform electric and magnetic field which are parallel to each other. The particle will move in a
Astraight line
Bcircle
Chelix
Dcycloid