A charge particle travels along a straight line with a speed v in region where both electric field E and magnetic field b are present.It follows that
|E|=|B| and the two field are perpendicular
|E|=v|B| and the two field are perpendicular
|B|=v|E| and the two field are parallel
|B|=v|E| and the two fields are perpendicular
The correct Answer is:B
Step by step video, text & image solution for A charge particle travels along a straight line with a speed v in region where both electric field E and magnetic field b are present.It follows that by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MAGNETIC FIELD AND FORCESBook:DC PANDEYChapter:MAGNETIC FIELD AND FORCESExercise:Taking it together
Explore 75 Videos
- MAGNETIC FIELD AND FORCESBook:DC PANDEYChapter:MAGNETIC FIELD AND FORCESExercise:Assertion and reason
Explore 20 Videos
- MAGNETIC FIELD AND FORCESBook:DC PANDEYChapter:MAGNETIC FIELD AND FORCESExercise:Medical entrance s gallery
Explore 59 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBook:DC PANDEYChapter:INTERFERENCE AND DIFFRACTION OF LIGHTExercise:Level 2 Subjective
Explore 5 Videos
- MAGNETICSBook:DC PANDEYChapter:MAGNETICSExercise:MCQ_TYPE
Explore 1 Video
Similar Questions
Knowledge Check
A charge q moves in a region where electric field E and the magnetic field B both exist, then the force on its is
Aq(v×B)BqE+q(v×B)CqB+q(B×v)DqB+q(E×v)In a region where both non-zero uniform electric field and magnetic field coexist, the path of a charged particle
Acan not be a circleBmay be a circleCmay be a straight lineDmay be a helixA charged particle is at rest in the region where magnetic field and electric field are parallel. The particle will move in a :
Astraight lineBcircleCellipseDnone of these
A fine pencil of β-particles, moving with a speed v, enters a region (region I), where a uniform electric field and a uniform magnetic field are both present. These β-particles then move into region II where only the magnetic field, (out of the two fields present in region I) exists. The path of the β-particles, in the two regions is as shown in the figure.
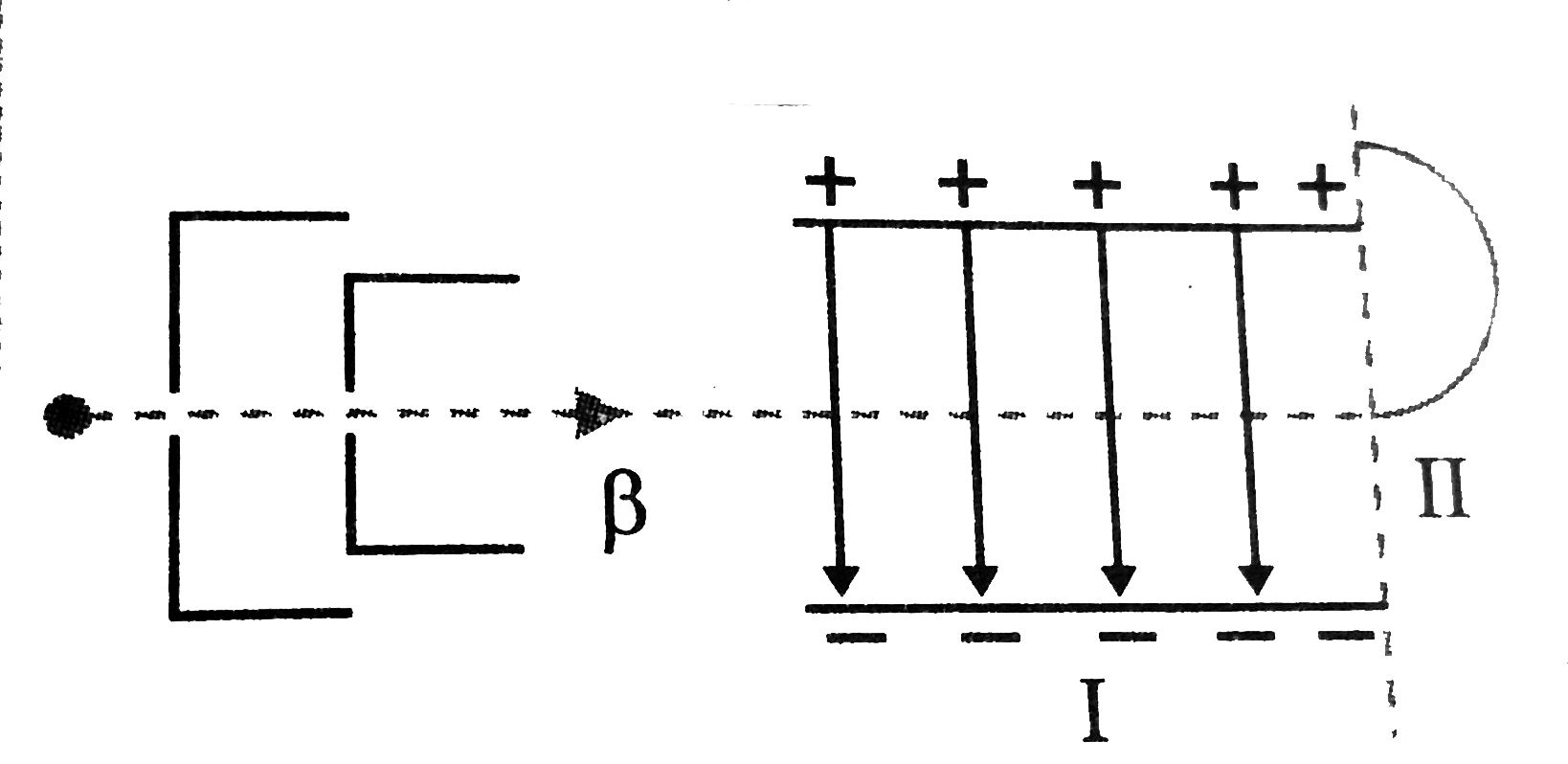
(i) state the direction of magnetic field.
(ii) state the relation between E and B in region I.
(iii) Drive the expression for the radius of the circular path of the β-particle in region II.
(iv) If the magnitude of magnetic field, in region II is changed to n times its earlier value, (without changing the magnetic field in region I) find the factor by which the radius of this circular path would change.
View SolutionIf a beam of electrons travels in a straight line in a certain region. Can we say there is no magnetic field?
View SolutionA charged particle moving with a uniform velocity →v enters a region where uniform electric and magnetic fields →E and →B are present. It passes through the region without any change in its velocity. What can we conclude about the (i) relative direction of →E, →V and →B? (ii) magnetic of →E and →B?
or
Find the condition under which the charged particle moving with different speeds in the presence of electric and magnetic field vectors can be used to select charged particles of a particular speeds.
View SolutionA charged particle, having a charge q, is moving with a speed v along the x-axis. It enters a region of space where an electric field →E(=Eˆj) and a magnetic field →B are both present. The particle, on emerging from this region, is observed to be moving along the x-axis only. Obtain an expression for the magnitude of →B in terms of v and E. Give the direction of →B.
View SolutionA charged particle is at rest in the region where magnetic field and electric field are parallel. The particle will move in a :
View Solution

