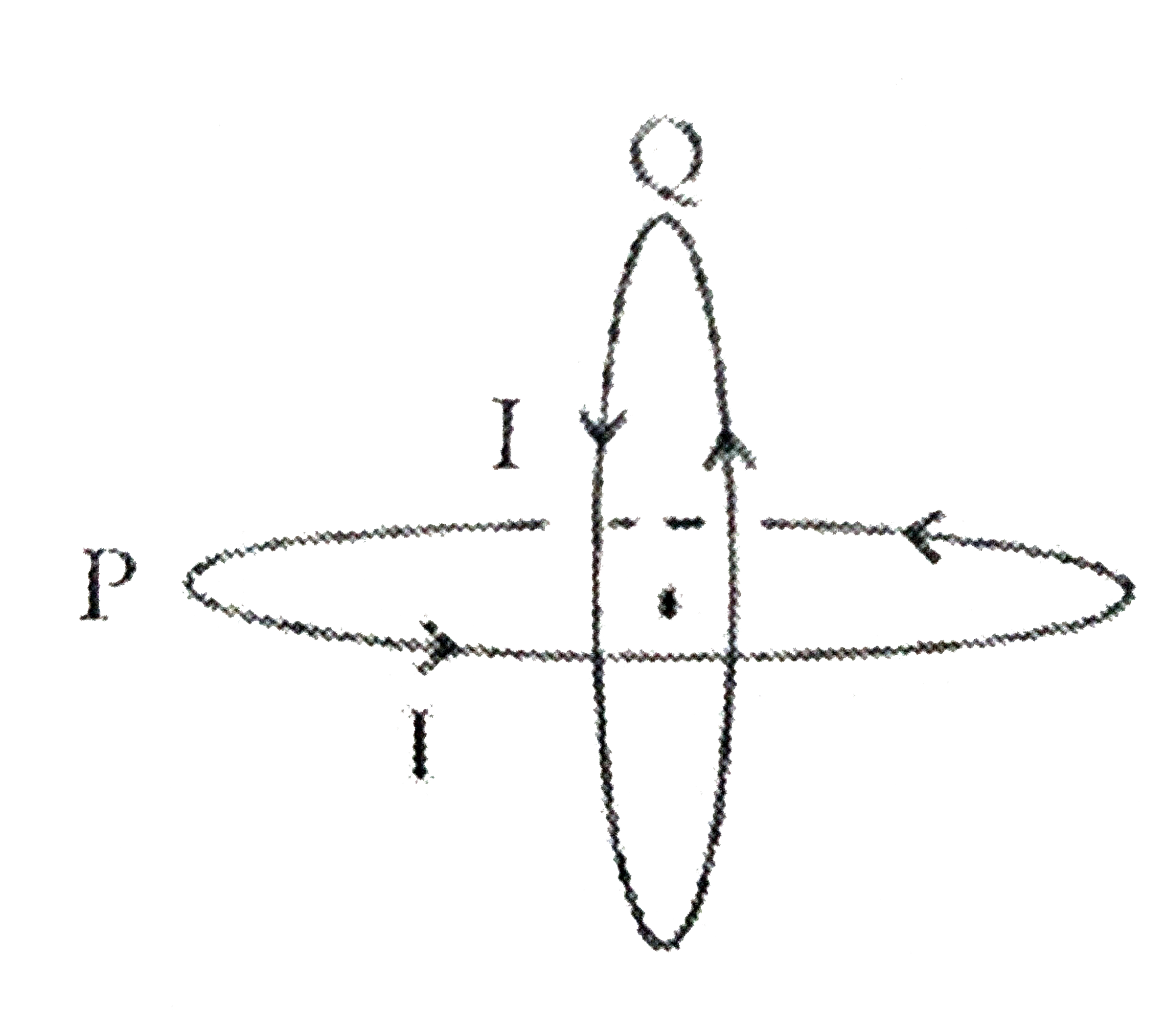
Two identical coils P and Q each of radius R are lying in perpendicular planes such that they have a common centre. Find the magnitude and PC direction of the magnetic field at the common centre of the two coils, if they carry currents equal to land √3I respectively.
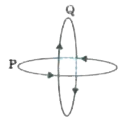
Magnetic field at the centre of current carrying loop P is given by :
B1=μ0I2πR , vertically upwards
Magnetic field at the centre of current carrying loop Q is given by :
B2=μ0√3I2πR, towards left
Net magnetic field at the common centre of loops will be :
Bnet=√B21+B22=
⎷(μ0I2πR)2+(μ0√3I2πR)2
=μ0I2πR√4=μ0IπR
Direction of magnetic field will be :
tanθ=B1B2=1√3
θ=30∘ .
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Revision Exercises (Long Answer Questions )
12 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Revision Exercises (Numerical Problems )
18 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Revision Exercises (Fill in the Blanks )
10 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
Similar Questions
Two identical loops P and Q each of radius 5cm are lying in perpendicular planes such that they have a common centre as shown in the figure. Find the magnitude and direction of the net field at the common centre of the two coils, if they carry currents equal to 3A and 4A respectively.
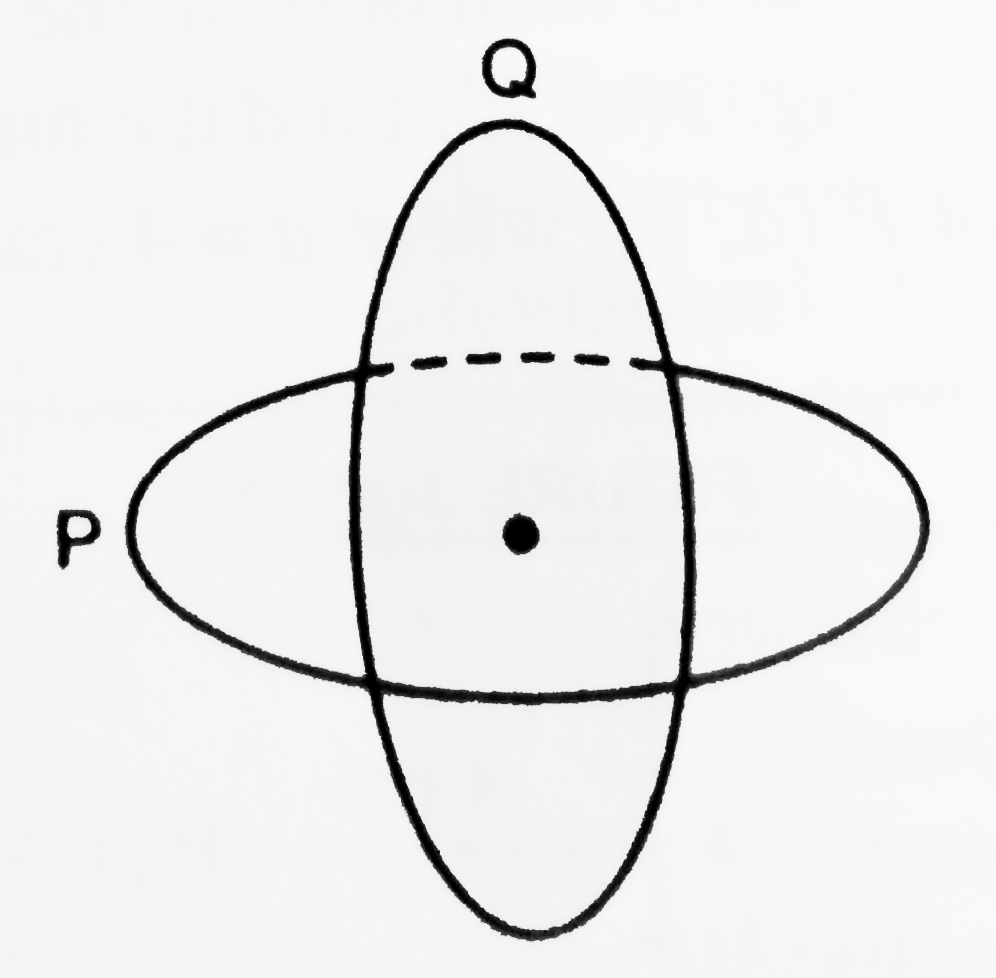
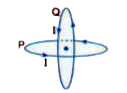
View SolutionTwo identical circular wires P and Q each of radius R and carrying current 'I' are kept in perpendicular planes such that they have a common centre as shown in fig. Find the magnitude and direction of the net magnetic field at the common centre of the two coils.
View Solution
Knowledge Check
The magnetic field at centre of a hexagonal coil of side l carrying a current I is
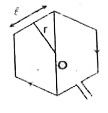 A√3μ0IπlBμ0I4πlCπμ0I√3lDzero
A√3μ0IπlBμ0I4πlCπμ0I√3lDzeroThe magnitude of the magnetic field at the centre of the tightly wound 150 turn coil of radius 12 cm carrying a current of 2 A is
A18GB19.7GC15.7GD17.7GTwo similar coils are kept mutually perpendicular such that their centres coincide. At the centre, find the ratio of the magnetic field due to one coil and the resultant magnetic field by both coils, if the same current is flown
A1:√2B1:2C2:1D√3:1
Two identical circular wires P and Q each of radius R and carrying current 'I' are kept in perpendicular planes such that they have a common centre as shown in the figure. Find the magnitude and direction of the net magnetic field at the common centre of the two coils.
View SolutionTwo identical coils each of radius 10cm and having number of turns 100 are lying in perpendicular planes, such that they have common centre. Find the resultant magnetic field at the centre of the coils if they carry currents 3A and 3√3A respectively.
View SolutionTwo identical circular coils, P and Q, carrying currents 1A and √3A respectively, are placed concentrically and perpendicular to each other lying in the XY and YZ plane. Find the magnitude and direction of the net magnetic field at the centre of the coils.
View Solution(a) State Biot - Savart law and express this law in the vactor form.
(b) Two identical circular coils, P and Q each of radius R, carrying currents 1A and √3A
respectively, are placed concentrically and perpendicular to each other lying in the XY
and YZ planes. Find the magnitude and direction of the net magnetic field at the centre
of the coils.
View SolutionTwo circular coils of radii 5.0 cm and 10 cm carry equal currents of 2.0 A. The coils have 50 and 100 turns respectively and are placed in such a way that their planes as well as the centres coincide. Find the magnitude of the magnetic field B at the common centre of the coils if the currents in the coils are (a) in the same sense (b) in the opposite sense.
View Solution
