(a) State Biot - Savart law and express this law in the vactor form.
(b) Two identical circular coils, P and Q each of radius R, carrying currents 1A and √3A
respectively, are placed concentrically and perpendicular to each other lying in the XY
and YZ planes. Find the magnitude and direction of the net magnetic field at the centre
of the coils.
Solution:
(a) Biot-Savart Law:
The Biot-Savart Law states that the magnetic field B produced at a point in space by a small segment of current-carrying wire is directly proportional to the current I flowing through the wire, the length of the wire segment dl, and the sine of the angle θ between the wire segment and the line connecting the wire segment to the point where the magnetic field is being calculated. The law can be mathematically expressed as:
dB=μ04π⋅Idl×rr3
Where:
- dB is the infinitesimal magnetic field produced by the current segment.
- μ0 is the permeability of free space.
- I is the current through the wire.
- dl is the length vector of the wire segment.
- r is the position vector from the wire segment to the point where the field is calculated.
- r is the magnitude of r.
In vector form, the Biot-Savart law can be expressed as:
B=μ04π∫Idl×rr3
(b) Finding the net magnetic field at the center of the coils:
1. Identify the magnetic field due to each coil at the center:
- For coil P (current IP=1A):
The magnetic field at the center of a circular coil is given by:
BP=μ0IP2R
- For coil Q (current IQ=√3A):
Similarly, the magnetic field at the center of coil Q is:
BQ=μ0IQ2R
2. Calculate the magnetic fields:
- For coil P:
BP=μ0⋅12R=μ02R
- For coil Q:
BQ=μ0⋅√32R=μ0√32R
3. Determine the direction of the magnetic fields:
- The magnetic field due to coil P (lying in the XY plane) will be in the positive Z direction (using the right-hand rule).
- The magnetic field due to coil Q (lying in the YZ plane) will be in the negative X direction (using the right-hand rule).
4. Express the magnetic fields in vector form:
- For coil P:
BP=μ02R^k
- For coil Q:
BQ=−μ0√32R^i
5. Calculate the net magnetic field:
- The net magnetic field Bnet at the center of the coils is the vector sum of BP and BQ:
Bnet=BP+BQ=μ02R^k−μ0√32R^i
6. Magnitude of the net magnetic field:
- The magnitude can be calculated using the Pythagorean theorem:
|Bnet|=
⎷(−μ0√32R)2+(μ02R)2
=√3μ204R2+μ204R2=√4μ204R2=μ0R
7. Direction of the net magnetic field:
- The direction can be found using the components. The net magnetic field vector can be expressed as:
Bnet=−μ0√32R^i+μ02R^k
- The direction can be represented in terms of angles or unit vectors based on the components.
- dB is the infinitesimal magnetic field produced by the current segment.
- μ0 is the permeability of free space.
- I is the current through the wire.
- dl is the length vector of the wire segment.
- r is the position vector from the wire segment to the point where the field is calculated.
- r is the magnitude of r.
- For coil P (current IP=1A):
The magnetic field at the center of a circular coil is given by:
Similarly, the magnetic field at the center of coil Q is:
- For coil P:
- The magnetic field due to coil P (lying in the XY plane) will be in the positive Z direction (using the right-hand rule).
- The magnetic field due to coil Q (lying in the YZ plane) will be in the negative X direction (using the right-hand rule).
- For coil P:
- The net magnetic field Bnet at the center of the coils is the vector sum of BP and BQ:
- The magnitude can be calculated using the Pythagorean theorem:
⎷(−μ0√32R)2+(μ02R)2
- The direction can be found using the components. The net magnetic field vector can be expressed as:
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SECTION-C
55 Videos
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - PHYSICS (Theory) DELHI BOARD -2016 [SET -I][COMPTT.]
12 Videos
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SECTION-A
31 Videos
- SAMPLE PAPER 2019BOOK - XII BOARDS PREVIOUS YEARCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
Two identical circular coils, P and Q each of radius R, carrying currents 1 A and √3 A respectively, are placed concentrically are perpendicualr to each other lying in the XY and YZ planes. Find the magnitude and direction of the net magnetic field at the centre of the coils.

View SolutionState Biot-Savart's law and express this law in the vector form.
View SolutionTwo identical circular coils, P and Q, carrying currents 1A and √3A respectively, are placed concentrically and perpendicular to each other lying in the XY and YZ plane. Find the magnitude and direction of the net magnetic field at the centre of the coils.
View SolutionBiot Savart's Law
View SolutionBiot savart's law
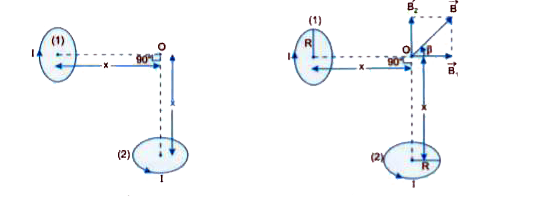
View SolutionTwo small identical circular loops, marked (1) and (2), carrying equal currents are placed with the geometrical axes perpendicular to each other as shown in the fig. Find the fig. Find the magnitude and direction of the net magnetic field at the net magnetic field at the point O.
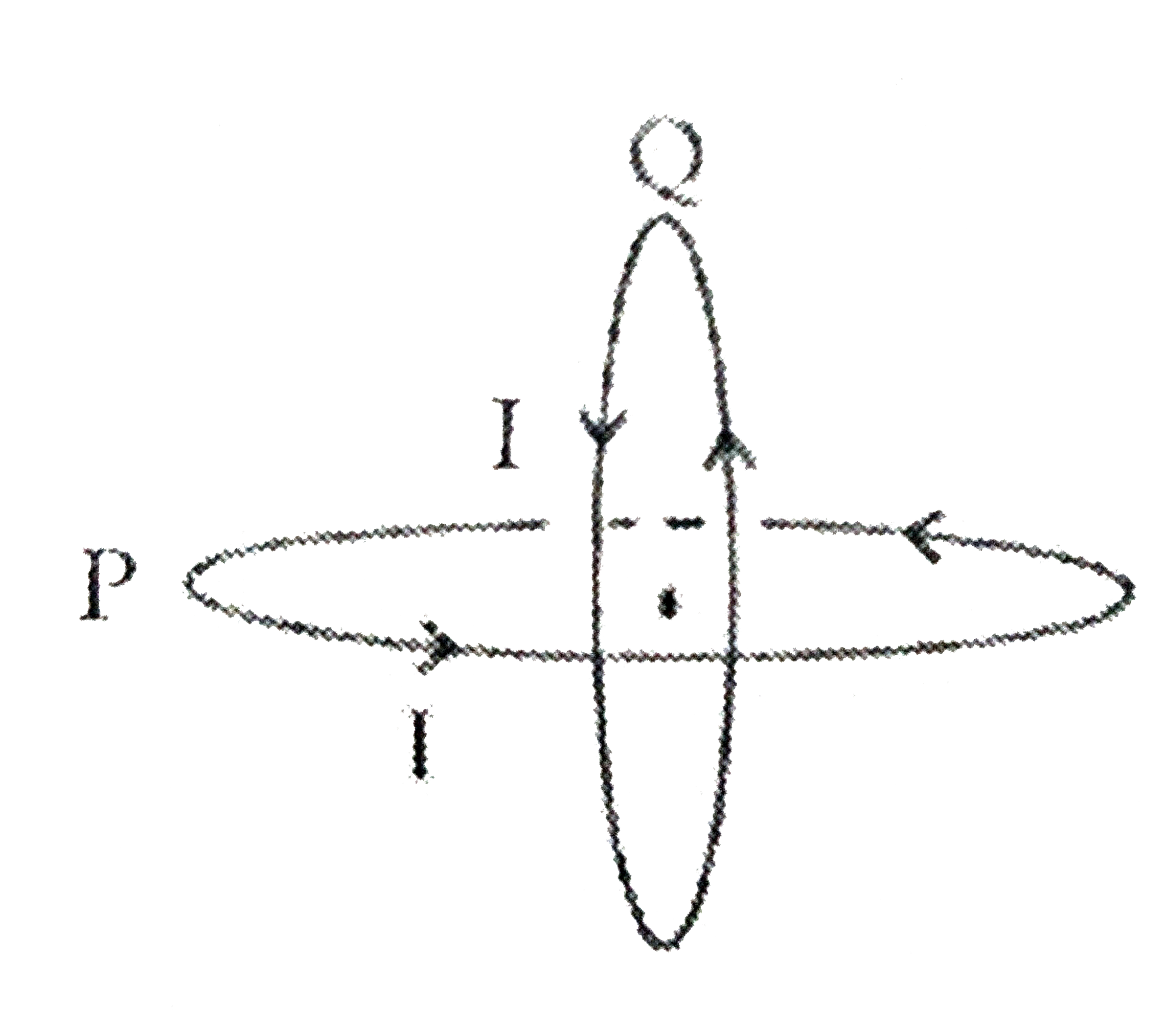
View SolutionTwo identical circular wires P and Q each of radius R and carrying current 'I' are kept in perpendicular planes such that they have a common centre as shown in the figure. Find the magnitude and direction of the net magnetic field at the common centre of the two coils.
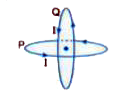
View SolutionTwo identical circular wires P and Q each of radius R and carrying current 'I' are kept in perpendicular planes such that they have a common centre as shown in fig. Find the magnitude and direction of the net magnetic field at the common centre of the two coils.
View SolutionFig shows two current-carrying wires 1 and 2. Find the magnitudes and directions of the magnetic field at points P,Q and R.

View SolutionTwo small circular loops, marked (1) and (2), carrying equal currents are placed with the geometrical axes perpendicular to each other as shown in figure. Find the magnitude and direction of the net magnetic field produced at the point O.
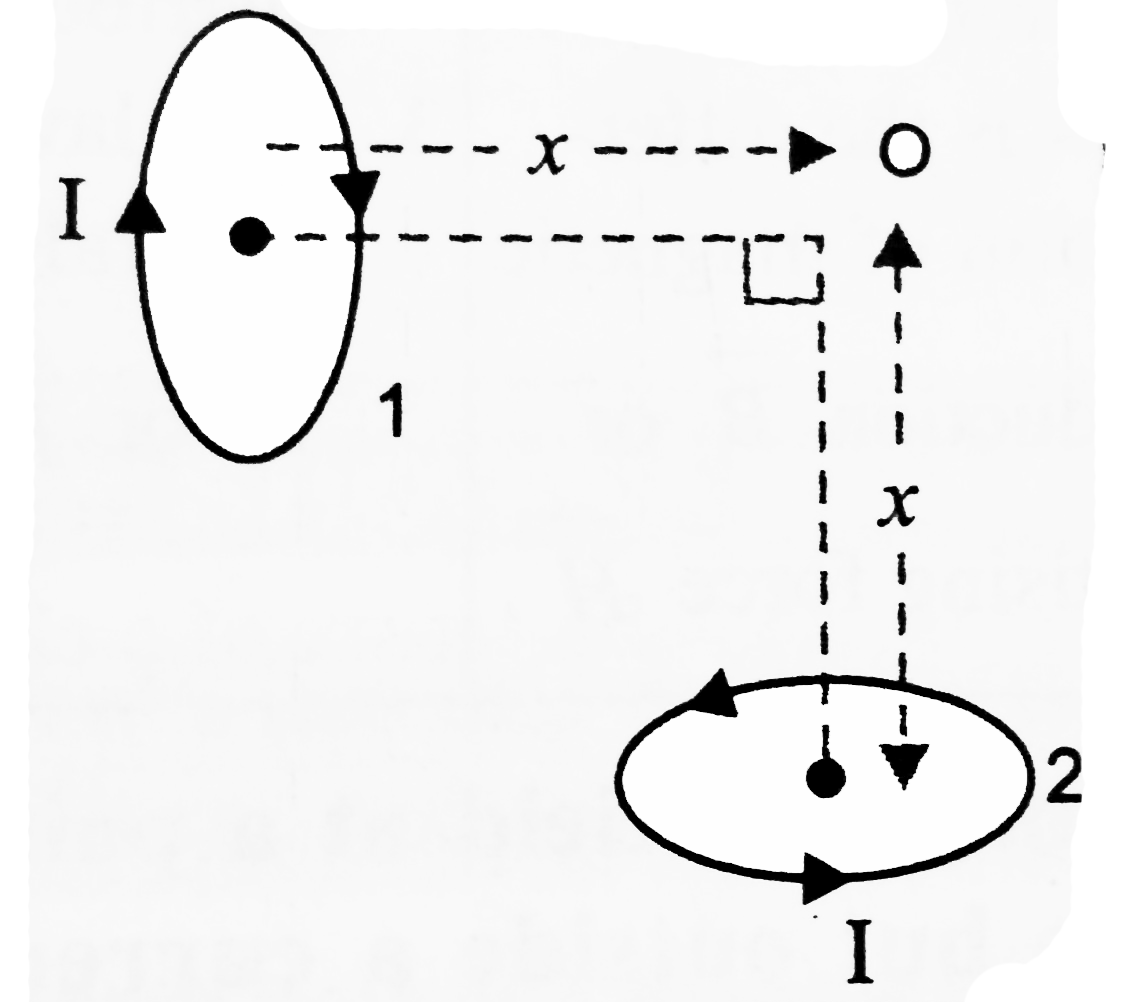
View Solution
