Particle is projected from the ground at a certain angle with horizontal . If particle takes time T to hit the ground again , then maximum height of the projectile is
T2g2
T2g4
T2g8
T2g5
The correct Answer is:C
To find the maximum height of a projectile that is projected from the ground at an angle with the horizontal and takes time T to hit the ground, we can follow these steps:
1. Identify the Components of Velocity:
- When a particle is projected at an angle θ with an initial velocity u, it has two components of velocity:
- Horizontal component: ux=ucosθ
- Vertical component: uy=usinθ
2. Time of Flight:
- The total time of flight (T) for a projectile is given by the formula:
T=2usinθg
- Here, g is the acceleration due to gravity.
3. Vertical Motion Analysis:
- The maximum height (H) reached by the projectile can be calculated using the vertical component of the initial velocity and the time taken to reach the maximum height.
- The time to reach the maximum height is half of the total time of flight:
t=T2
4. Using the Equation of Motion:
- The maximum height can be calculated using the formula:
H=uy⋅t−12gt2
- Substituting uy=usinθ and t=T2:
H=(usinθ)⋅(T2)−12g(T2)2
5. Simplifying the Expression:
- Substitute t=T2:
H=(usinθ)⋅T2−12g⋅T24
- This simplifies to:
H=usinθT2−gT28
6. Relating Initial Velocity to Time of Flight:
- From the time of flight equation, we can express usinθ:
usinθ=gT2
- Substitute this back into the height equation:
H=(gT2)T2−gT28
- This simplifies to:
H=gT24−gT28
7. Final Calculation:
- Combine the terms:
H=2gT28−gT28=gT28
Conclusion:
The maximum height H of the projectile is given by:
H=gT28
- When a particle is projected at an angle θ with an initial velocity u, it has two components of velocity:
- Horizontal component: ux=ucosθ
- Vertical component: uy=usinθ
- The total time of flight (T) for a projectile is given by the formula:
T=2usinθg
- Here, g is the acceleration due to gravity.
- The maximum height (H) reached by the projectile can be calculated using the vertical component of the initial velocity and the time taken to reach the maximum height.
- The time to reach the maximum height is half of the total time of flight:
t=T2
- The maximum height can be calculated using the formula:
H=uy⋅t−12gt2
- Substituting uy=usinθ and t=T2:
H=(usinθ)⋅(T2)−12g(T2)2
- Substitute t=T2:
H=(usinθ)⋅T2−12g⋅T24
- This simplifies to:
H=usinθT2−gT28
- From the time of flight equation, we can express usinθ:
usinθ=gT2
- Substitute this back into the height equation:
H=(gT2)T2−gT28
- This simplifies to:
H=gT24−gT28
- Combine the terms:
H=2gT28−gT28=gT28
The maximum height H of the projectile is given by:
H=gT28
Topper's Solved these Questions
- MOTION IN A PLANE Book:MODERN PUBLICATIONChapter:MOTION IN A PLANE Exercise:COMPETITION FILE OBJECTIVE TYPE QUESTIONS (B. Multiple Choice Questions)
Explore 38 Videos
- MOTION IN A PLANE Book:MODERN PUBLICATIONChapter:MOTION IN A PLANE Exercise:COMPETITION FILE OBJECTIVE TYPE QUESTIONS (JEE (Main) & Other Boards for Engineering Entrance)
Explore 14 Videos
- MOTION IN A PLANE Book:MODERN PUBLICATIONChapter:MOTION IN A PLANE Exercise:Revision Exercises (Numerical Problems)
Explore 26 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:MODERN PUBLICATIONChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Chapter Practise Test
Explore 16 Videos
- MOTION IN A STRAIGHT LINE Book:MODERN PUBLICATIONChapter:MOTION IN A STRAIGHT LINE Exercise:CHAPTER PRACTICE TEST
Explore 16 Videos
Similar Questions
A particle is projected from the ground with speed u un such a manner that its range is found to be two times the maximum height . If range of the projectile can be written as nu25g , then what is the value of n ?
View SolutionA particle is projected form ground with velocity u ar angle θ from horizontal. Match the following two columns.
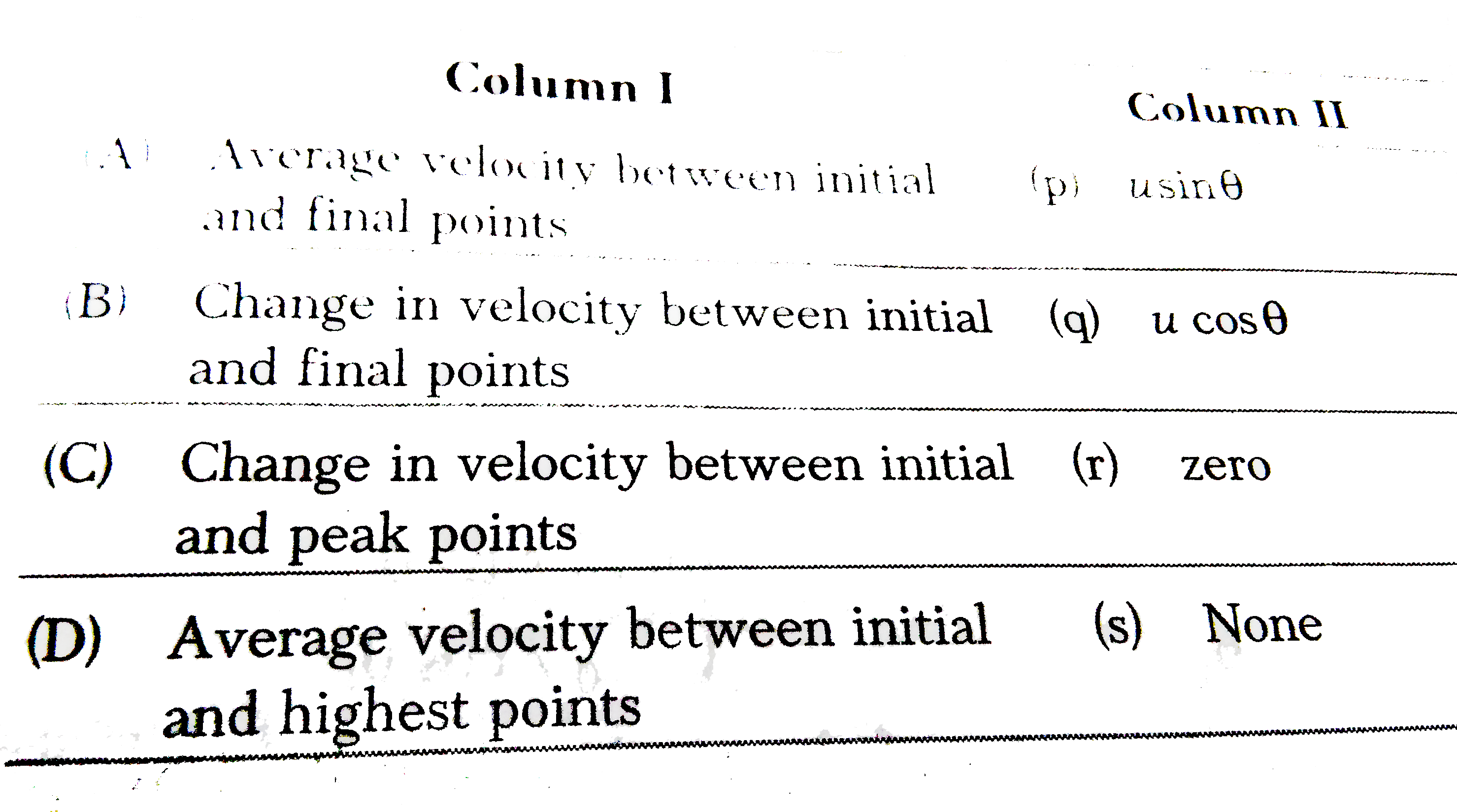
View Solution
Knowledge Check
A projectile is projected from the ground by making an angle of 60∘ with the horizontal. After 1 s projectile makes an angle of 30∘ with the horizontal . The maximum height attained by the projectile is (Take g=10ms−2)
A452mB454mC432mD434mA particle is pojected from the ground at an angle of θ with the horizontal with an initial speed of u. Time after which velocity vector of the projectile is perpendicular to the initial velocity is
Au/(gsinθ)Bu/(gcosθ)C2ugsinθD2utanθA projectile is projected from the ground making an angle of 30∘ with the horizontal.Air exerts a drag which is proportional to the velocity of the projectile
Aat highest point velocity will be horizontalBthe time of ascent will be equal to the time of descentCThe time of descent will be greater than the time of ascentDthe time of ascent will be greater than the time of descent
A particle is projected from point A on the ground at an angle θ with horizontal. Another particle is projected from point B simultaneously from height 4H above point A with same velocity A and B are in the same vertical plane, where H is the maximum height attained by the particle A, Both the particle collide at the same time on the ground. Find the angle at which particle B is projected with hoizontal.
View SolutionA particle is projected from the ground with an initial speed of v at an angle θ with horizontal. The average velocity of the particle between its point of projection and highest point of trajectroy is :
View SolutionA particle is projected from ground with speed u and at an angle θ with horizontal. If at maximum height from ground, the speed of particle is 1/2 times of its initial velocity of projection, then find its maximum height attained.
View SolutionA particle is projected from ground at some angle with the horizontal. Let P be the point at maximum height H. At what height above the point P should the particle be aimed to have equal to maximum height ?
View SolutionA particle is projected from the ground with velocity u at angle θ with horizontal.The horizontal range,maximum height and time of flight are R,H and T respectively.Now keeping u as fixed, θ is varied from 30∘ to 60∘.Then
View Solution