A trolley is moving with velocity v1 in the horizontal direction . A bullet is fired from his trolley in the upward direction with a speed v2 . Observer is standing on the ground and observes the bullet to be moving in a parabolic path. What will be the range of projectile ?
2v1v2g
2v21g
2v22g
v1v2g
The correct Answer is:A
To solve the problem of finding the range of the projectile (the bullet) fired from a moving trolley, we can follow these steps:
1. Understanding the Motion:
- The trolley is moving horizontally with a velocity v1.
- The bullet is fired vertically upward with a speed v2.
- An observer on the ground sees the bullet moving in a parabolic path due to the combination of its vertical and horizontal velocities.
2. Components of Velocity:
- The bullet has two components of velocity:
- Vertical component: v2 (upward)
- Horizontal component: v1 (due to the motion of the trolley)
3. Time of Flight:
- The time of flight T for the bullet can be calculated using the vertical motion equations.
- The bullet will go up and then come down. The time to reach the maximum height can be calculated using:
Tup=v2g
- The total time of flight T (up and down) will be:
T=2×Tup=2×v2g=2v2g
4. Horizontal Range:
- The horizontal range R can be calculated using the horizontal velocity and the total time of flight:
R=v1×T
- Substituting the expression for T:
R=v1×2v2g
- Therefore, the range of the projectile is:
R=2v1v2g
Final Answer:
The range of the projectile (bullet) is given by:
R=2v1v2g
- The trolley is moving horizontally with a velocity v1.
- The bullet is fired vertically upward with a speed v2.
- An observer on the ground sees the bullet moving in a parabolic path due to the combination of its vertical and horizontal velocities.
- The bullet has two components of velocity:
- Vertical component: v2 (upward)
- Horizontal component: v1 (due to the motion of the trolley)
- The time of flight T for the bullet can be calculated using the vertical motion equations.
- The bullet will go up and then come down. The time to reach the maximum height can be calculated using:
Tup=v2g
- The total time of flight T (up and down) will be:
T=2×Tup=2×v2g=2v2g
- The horizontal range R can be calculated using the horizontal velocity and the total time of flight:
R=v1×T
- Substituting the expression for T:
R=v1×2v2g
- Therefore, the range of the projectile is:
R=2v1v2g
The range of the projectile (bullet) is given by:
R=2v1v2g
Topper's Solved these Questions
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - COMPETITION FILE OBJECTIVE TYPE QUESTIONS (B. Multiple Choice Questions)
38 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - COMPETITION FILE OBJECTIVE TYPE QUESTIONS (JEE (Main) & Other Boards for Engineering Entrance)
14 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Revision Exercises (Numerical Problems)
26 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Chapter Practise Test
16 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
Similar Questions
A large number of bullets are fired in all directions with the same speed v. Find the maximum area on the ground on which these bullets will spread.
View SolutionA particle is projected from a stationary trolley. After projection, the trolley moves with a velocity 2(√15)m/s. For an observer on the trolley, the direction of the particle is as shown in the figure while for the observer on the ground, the ball rises vertically. The maximum height reached by the ball from the trolley is h meter. The value of h will be .......... .

View Solution
Knowledge Check
A shell is fired vertically upwards with a velocity v1 from a trolley moving horizontally with velocity v2. A person on the the ground observes the motion of the shell as a parabole, whose horizontal range is
A2v21v2gB2v21gC2v22gD2v1v2gA shell is fired vertically upwards with a velocity v1 from the deck of a ship travelling at a speed of v2 . A person on the shore observes the motion of the shell as parabola. Its horizontal range is given by:
A2v2gB2v1v22gC2v1v2gD2v21v22gA bullet of mass 20 gm is fired in the horizontal direction with a velocity 150 mis from a pistol of mass 1 kg. Recoil velocity of the pistol is
A3 m/sB3 km/sC300 m/sD1/3 m/s
Two trolleys A and B are moving with accelerations a and 2a, respectively, in the same direction. To an observer in trolley A. Find the magnitude of the pseudo force acting on a block of mass m on trolley B.
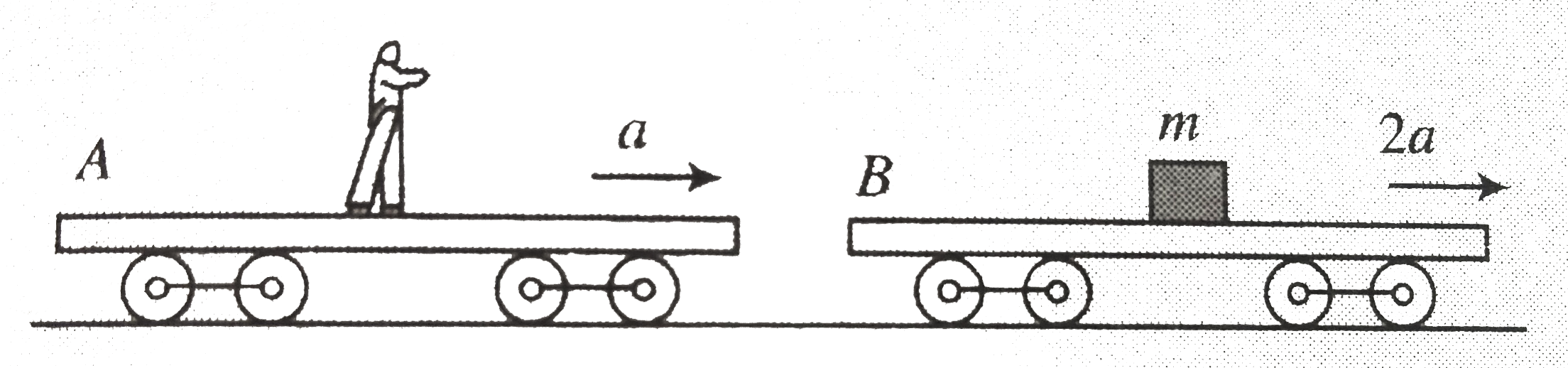
View SolutionA trolley was moving horizontally on a smooth ground with velocity v with respect to the earth. Suddenly a man starts running from rear end of the trolley with a velocity (3/2)v with respect to the trolley. After reaching the other end, the man turns back and continues running with a velocity (3/2)v with respect to trolley in opposite direction. If the length of the trolley is L, find the displacement of the man with respect to earth when he reaches the starting point on the trolley. Mass of the trolley is equal to the mass of the man.
View SolutionSeveral bullets are fired from a particular gun in various possible directions . If bullets are fired with a speed u, then maximum area of ground covered by the bullets is
View SolutionA trolley moves in horizontal direction with an acceleration a. A simple pendulum of length l is suspended from the roof of the trolley. The time period of the pendulum will be
View SolutionIn fig., blocks A and B move with velocities v1 and v2 along horizontal direction. Find the ratio of v1/v2
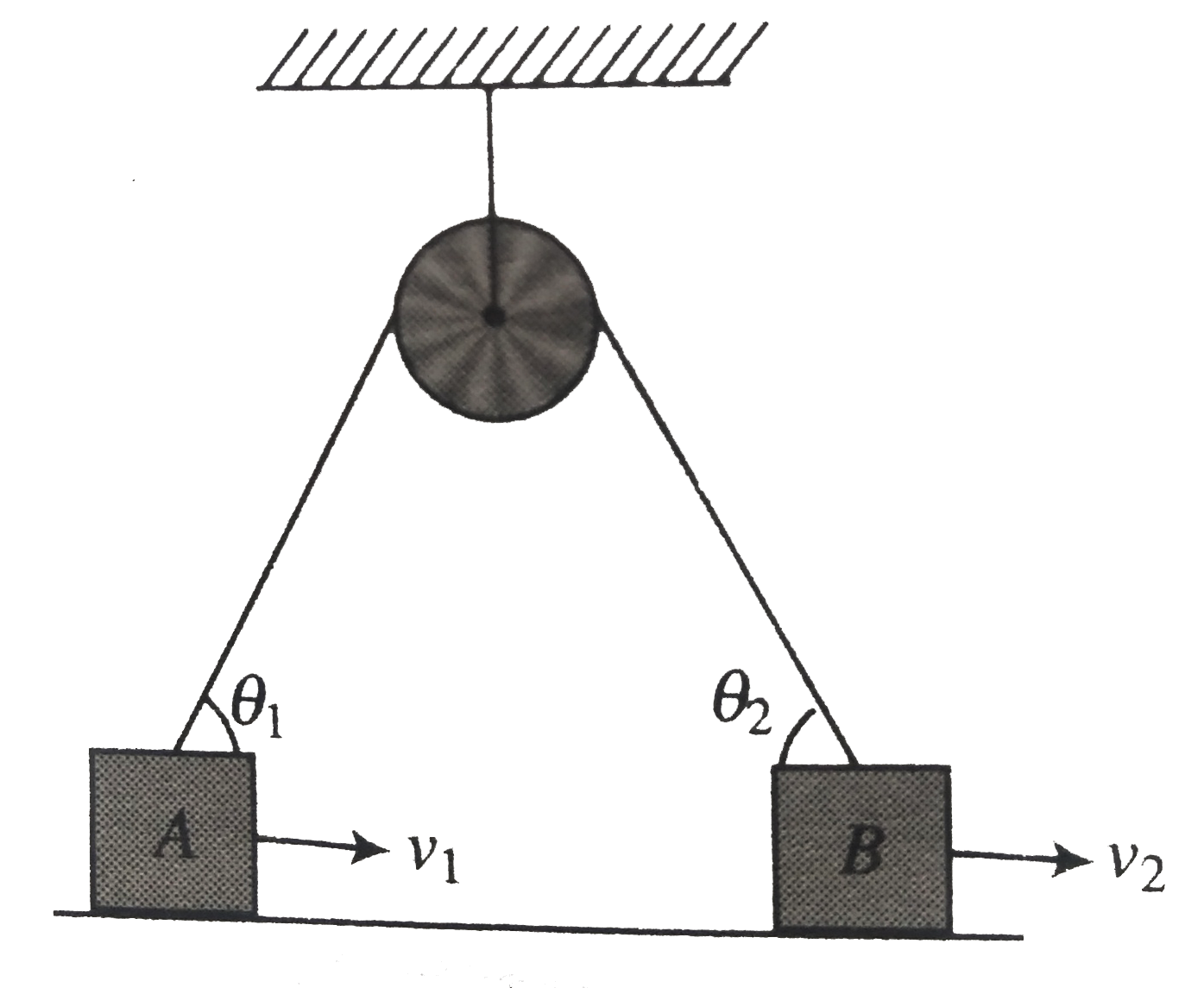
View Solution
