A particle is projected from ground at some angle with the horizontal. Let be the point at maximum height . At what height above the point should the particle be aimed to have equal to maximum height ?
H
2 H
H//2
3 H
The correct Answer is:A
(a)
We have to find .
From the figure in previous question, we know that if , then
Now
.
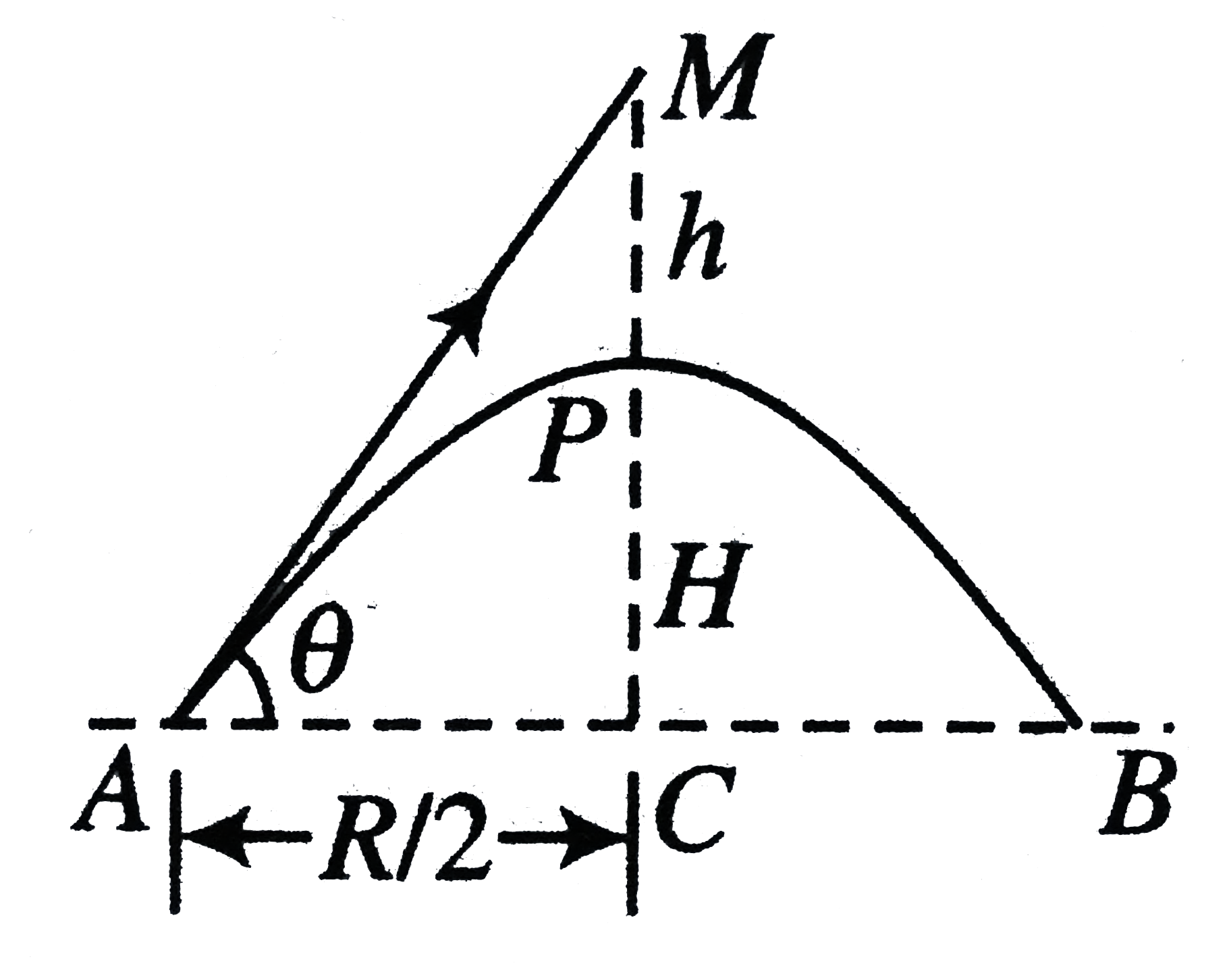 .
.
Topper's Solved these Questions
- KINEMATICS-2Book:CENGAGE PHYSICSChapter:KINEMATICS-2Exercise:Exercise Multiple Correct
Explore 11 Videos
- KINEMATICS-2Book:CENGAGE PHYSICSChapter:KINEMATICS-2Exercise:Exercise Assertion - Reasoning
Explore 5 Videos
- KINEMATICS-2Book:CENGAGE PHYSICSChapter:KINEMATICS-2Exercise:Exercise Subjective
Explore 40 Videos
- KINEMATICS-1Book:CENGAGE PHYSICSChapter:KINEMATICS-1Exercise:Integer
Explore 9 Videos
- KINETIC THEORY OF GASESBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASESExercise:Compression
Explore 2 Videos
Similar Questions
A particle is projected from point A on the ground at an angle θ with horizontal. Another particle is projected from point B simultaneously from height 4H above point A with same velocity A and B are in the same vertical plane, where H is the maximum height attained by the particle A, Both the particle collide at the same time on the ground. Find the angle at which particle B is projected with hoizontal.
View SolutionA particle is projected from the ground with velocity u at angle θ with horizontal.The horizontal range,maximum height and time of flight are R,H and T respectively.Now keeping u as fixed, θ is varied from 30∘ to 60∘.Then
View Solution
Knowledge Check
Particle is projected from the ground at a certain angle with horizontal . If particle takes time T to hit the ground again , then maximum height of the projectile is
AT2g2BT2g4CT2g8DT2g5A particle is projected from ground at an angle θ with horizontal with speed u. The ratio of radius of curvature of its trajectory at point of projection to radius of curvature at maximum height is -
A1sin2θcosθBcos2θC1sin3θD1cos3θA particle is projected from ground with speed u and at an angle θ with horizontal. If at maximum height from ground, the speed of particle is 1/2 times of its initial velocity of projection, then find its maximum height attained.
Au2gB2u2gCu22gD3u28g
A particle is projected from ground with some initial velocity making an angle of 45∘ with the horizontal. It reaches a height of 7.5m above the ground while it travels a horizontal distance of 10m from the point of projection. The initial speed of the projection is
View SolutionAt what angle to the horizontal should an object be projected so that the maximum height reached is equal to the horizontal range.
View SolutionA particle of mass m is projected with an initial velocity U at an angle θ to the horizontal. The torque of gravity on projectile at maximum height about the point of projection is
View SolutionA particle of mass m is projected with a velocity v making an angle of 45° with the horizontal. The magnitude of the angular momentum of the projectile about the point of projection, when the particle is at its maximum height h, is
View SolutionA particle of mass m is projected with a velocity v making an angle of 45∘ with the horizontal. The magnitude of the angular momentum of the projectile abut the point of projection when the particle is at its maximum height h is.
View Solution

