What is the magnetic field along the axis and equatorial line of a bar magnet ? Solution in Tamil
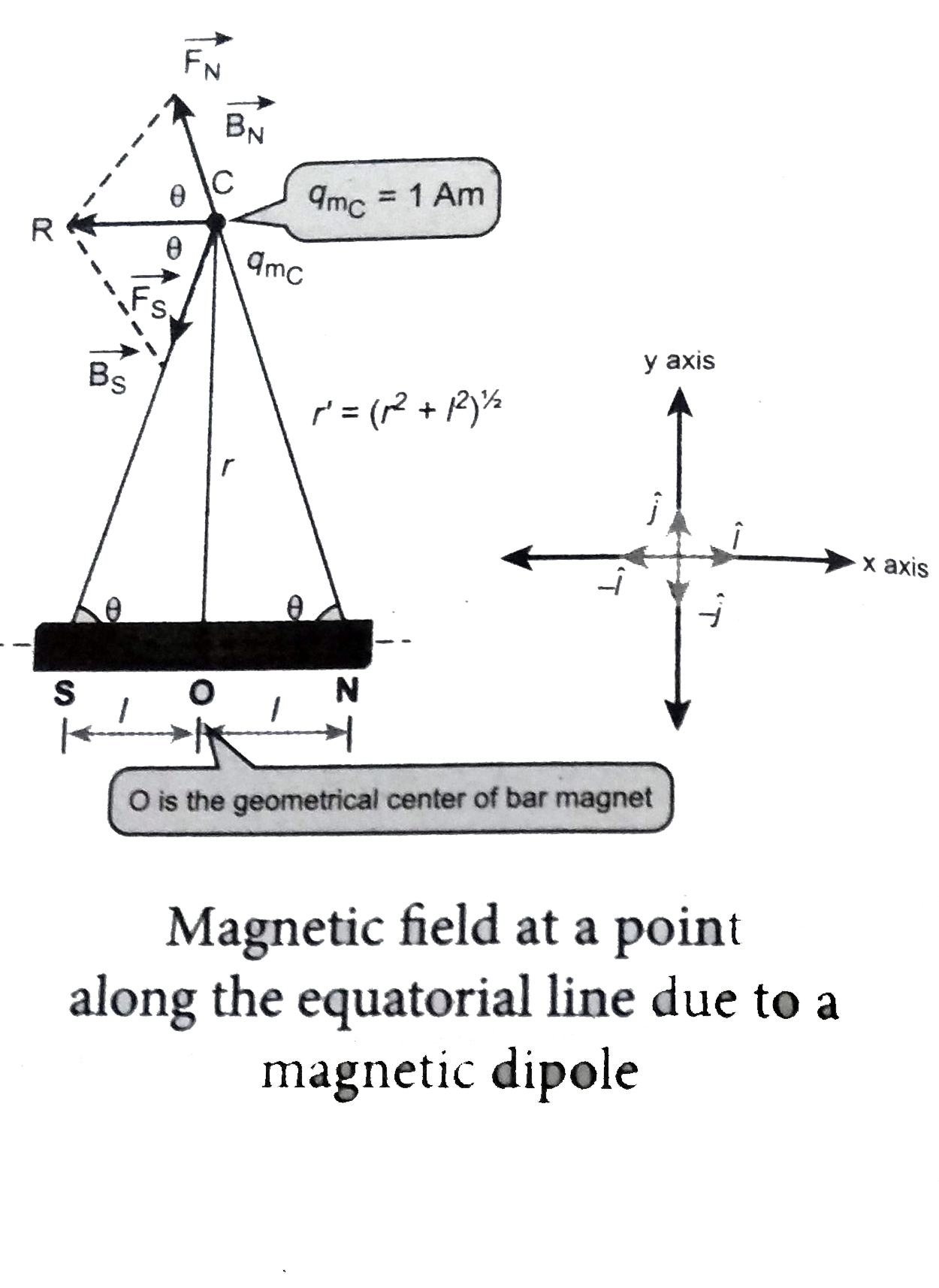
Magnetic field at a point along the equatorial line due to a magnetic dipole (bar magnet) Consider a bar magnet NS. Let N be the north pole and be the south pole of the bar magnet, each with pole strength qmand separated by a distance of 2l. The magnetic field (lies along the equatorial line) at a distance r from the geometrical center of the bar mao can be computed by keeping unit north pole(qmC=1Am) at C. The force experience the unit north pole at C due to pole strength N-S can be computed using Coulomb.s law of magnetism as follows:
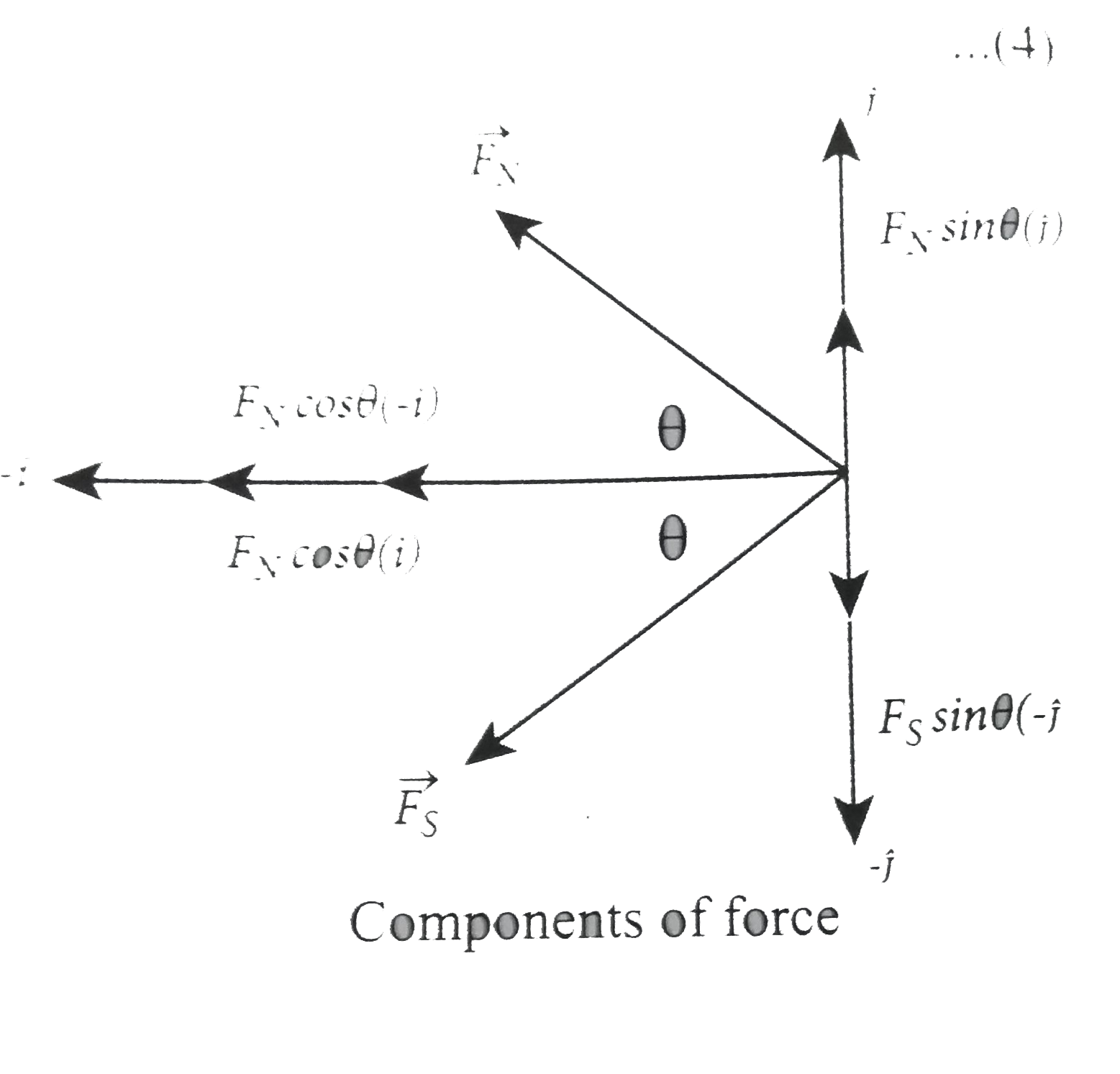
The force of. repulsion between North Pole of the bar magnet and unit north pole at point (in free space) is →F=−FNcosθˆi+FNsinθˆj
Where FN=μ0qm4πr1/2
The force of attraction (in free space) between south pole of the bar magnet and unit north pole at point C
→s=−FScosθˆi−Fssinθj.......(2)
Where FS=μ0qm4πr1/2
From equation (1) and equation (2), the net force at point Cis →F=→FN+Fs . This net force is equal to the magnetic field at the point C.
→B=−2μ04πqmr’2cosθˆi=−2μ04πqm(r2+l2)cosθˆi
In a right angle triangle NOC as shown in the Figure 1 cosθ=adjacenthypoteνse=1r’=1(r2+l2)12
Substituting equation 4 in equation 3 we get
→B=−μ0qm×(2l)4π(r2+l2)32ˆi......(5)
Since, magnitude of magnetic dipole moment is ∣∣→Pm∣∣=Pm=qm.2l and substituting in equation (5), the magnetic field at a point C
→Bequa→rial=−μ04πPm(r2+l2)32ˆi......(6)
compared to the distance between geometrical center of bar magnet and the location of point Ci.e.,r>>, then,
(r2+l2)32=r3...(7).
Therefore, using equation (7) in equation (6), we get
→Bequa→rial=−μ04πPmr3ˆi
Since Pmˆi=→Pm, in general, the magnetic field at equatorial point is given by
→Bequa→rial=−μ04πPmr3.......(8)
Note that magnitude of Barial is twice that of magnitude of Bequa→rial and the direction of Baξaland Bequa→rialare opposite.
Topper's Solved these Questions
- SAMPLE PAPER-05 ( SOLVED ) Book:FULL MARKSChapter:SAMPLE PAPER-05 ( SOLVED ) Exercise:PART-III
Explore 9 Videos
- SAMPLE PAPER 9Book:FULL MARKSChapter:SAMPLE PAPER 9Exercise:PART-IV
Explore 10 Videos
- SAMPLE PAPER-07 (SOLVED )Book:FULL MARKSChapter:SAMPLE PAPER-07 (SOLVED )Exercise:(PART - IV)(Answer all the questions.)
Explore 10 Videos
Similar Questions
Give the relation between electric field and electric potential .
View SolutionHow do we determine the electric field due to a continuous charge distribution ? Explain. Electric field due to continous charge distribution
View SolutionCalculate the electric field due to a dipole on its equatorial plane. (OR) Electric field due to an electric dipole at a point on the equatorial plane
View SolutionOn equatorial line of bar magnet, what is the formula for magnetic field strength?
View SolutionMagnetic field strength due to a short bar magnet on its axial line at a distance x is B. What is its value at the same distance on the equatorial line?
View SolutionThe time period of a bar magnet oscillating in a uniform magnetic field is 3 seconds. if the magnet is cut into two equal parts along the equatorial line of the magnet and one part is made to vibrate in the same field, what is the time period ?
View SolutionDefine equatorial line of a bar magnet.
View SolutionConsider a point on an equatorial axis of a short bar magnet. The direction of magnetic field at that point is
View SolutionMagnetic field at a distance x along the axis of a short bar magnet is
View SolutionWhat is the magnetic field along the axis and equatorial line of a bar magnet ?
View SolutionWhat is the magnetic field along the axis and equatorial line of a bar magnet ?
View SolutionWhat is the magnetic field along the axis and equatorial line of a bar magnet ?
View SolutionWhat is the magnetic field along the axis and equatorial line of a bar magnet ?
View SolutionWrite an expression of magnitude of magnetic field at point lies on equatorial line of a bar magnet.
View SolutionWhat is the magnetic moment of each piece when a bar magnet of moment 'M' is cut into two equal parts (i) along its axis and (ii) along its equatorial line.
View Solution