Locate the image of the point object O in the situtaion shown. The point C denotes the centre of curvature of the separating surface. Solution in Tamil
Give: u = - 15 cm, R = 30 cm, n1=1andn2 = 1.5 Equation for single spherical surface is n2v−n3u=(n2−n1R)
Substituing the vlues, 1.5v−1−15=(1.5−1)30:1.5v+115=0.530
1.5v+115=1601.5v=160−115,
1.5v=1−460=−360,=−120
The image is a virtual image formed 30 cm to the spherical surface.

Topper's Solved these Questions
- OPTICSBOOK - FULL MARKSCHAPTER - OPTICSEXERCISE - TEXTUAL EVALUATION SOLVED ( MULTIPLE CHOICE QUESTIONS : )
20 Videos
- OPTICSBOOK - FULL MARKSCHAPTER - OPTICSEXERCISE - TEXTUAL EVALUATION SOLVED SHORT ANSWER QUESTION
80 Videos
- MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENT BOOK - FULL MARKSCHAPTER - MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENT EXERCISE - ADDITIONAL QUESTIONS SOLVED - NUMERICAL PROBLEMS :
4 Videos
- RECENT DEVELOPMENTS IN PHYSICSBOOK - FULL MARKSCHAPTER - RECENT DEVELOPMENTS IN PHYSICSEXERCISE - ADDITIONAL QUESTIONS (Short Answer Question)
6 Videos
Similar Questions
The speed of light in an isotropic medium depends on,
View SolutionState the laws of reflection.
View SolutionThe radius of the first orbit of hydrogen atom is 0.5 Å. The electron moves is an orbit with a uniform speed of 2.2×106ms−1. What is the magnetic field produced at the centre of the uncleus due to the mation of this electron ? Use μ0=4π×10−7Hm−1 and electric charge =1.6×10−19 C
View SolutionWhat is physics?
View SolutionA spherical surface of radius of curvature R separates air (refractive index 1.0) from glass (refractive index 1.5). The centre of curvature is in the glass. A point object P placed in air is found to have a real image Q in the glass. The line PQ cuts the surface at a point O, and PO=OQ. The distance PO
View SolutionIn the figure, a point object O is placed in air. A spherical boundry separates two media of radius of curvature 1.0m. AB is principal axis. The separation between the images formed due to refraction at spherical surface is

View SolutionA spherical surface of radius of curvature R separates air (refractive index 1.0) from glass (refractive index 1.5). The center of curvature is in the glass. A point object P placed in air is found to have a real image Q in the glass. The ling PQ cuts the surface at a point O, and PO=OQ. The distance PO is equal to
View SolutionLocate the image of the point object O . The point C is centre of curvature of the spherical surface.
View SolutionTwo cancave refracting surfacwe of equal radii fo curvature face each other in air as shown in figure. A point object O is placed midway between the centre and one of the poles. Then the separation between the images of O formed by each refracting surface is
View Solutionचित्र में दिखाई गई परिस्थिति में वस्तु O के प्रतिबिंब का स्थान निर्धारित करें । बिंदु C दोनों माध्यमों की उभयनिष्ठ (COMMON) गोलीय सतह का वक्रता - केंद्र हैं ।
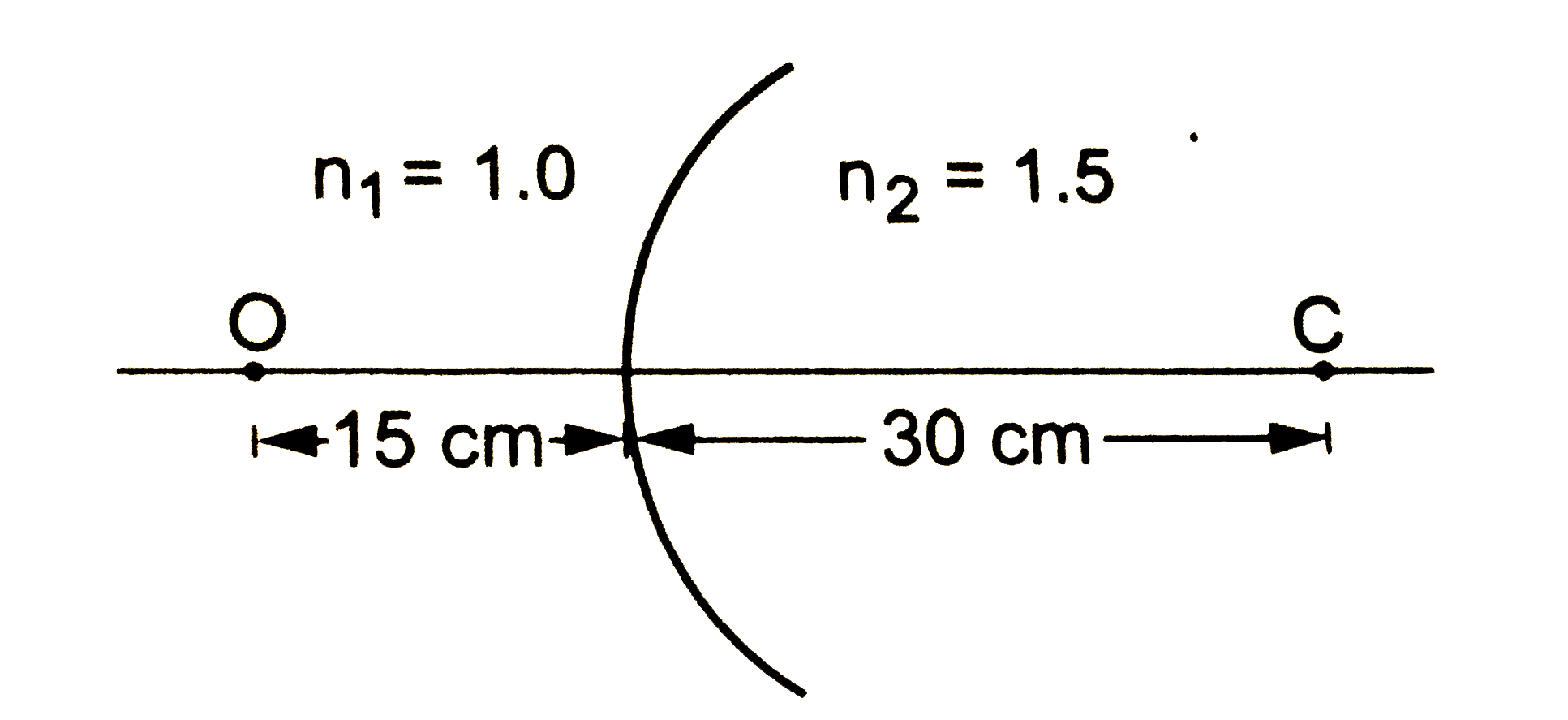
View SolutionA spherical surface of radius of curvature R, separates air (refractive index 1.0) fromglas (refractive index 1.5). The centre of curvature is in the glass. A point object P in air is found to have a real image Q in the glass.The line PQ cuts the surface at a point O and PO =OQ. The distance PO is equal to
View Solution(a) A point object, O is on the principle axis of a spherical surface having a radius of curvature, R. Draw a diagram to obtain the relation between the object and image distances, the refractive indicess of the media and the radius of curvature of the spherical surface.
View SolutionLocate the image of the point object O in the situation shown in figure. The point C denotes the centre of curvature of the separating surface.

View SolutionLocate the image formed by refraction in the situation shown in figure. The point C is the centre of curvature

View SolutionA spherical surface of radius of curvature R, separates air (refractive index 1.0) from glass (refractive index 1.5) The centre of curvature is in the glass. A point object P placed in air is found to have a real image Q in the glass. The line PQ cuts the surface at a point O and PO=OQ. The distance PO is equal to
View Solution
