From a point P outside a circle with centre at C, tangents PA and PB are drawn such that 1(CA)2+1(PA)2=116, then the length of chord AB is
6
8
4
12
The correct Answer is:B
tanθ=rPA
Given, 1r2+1PA2=116
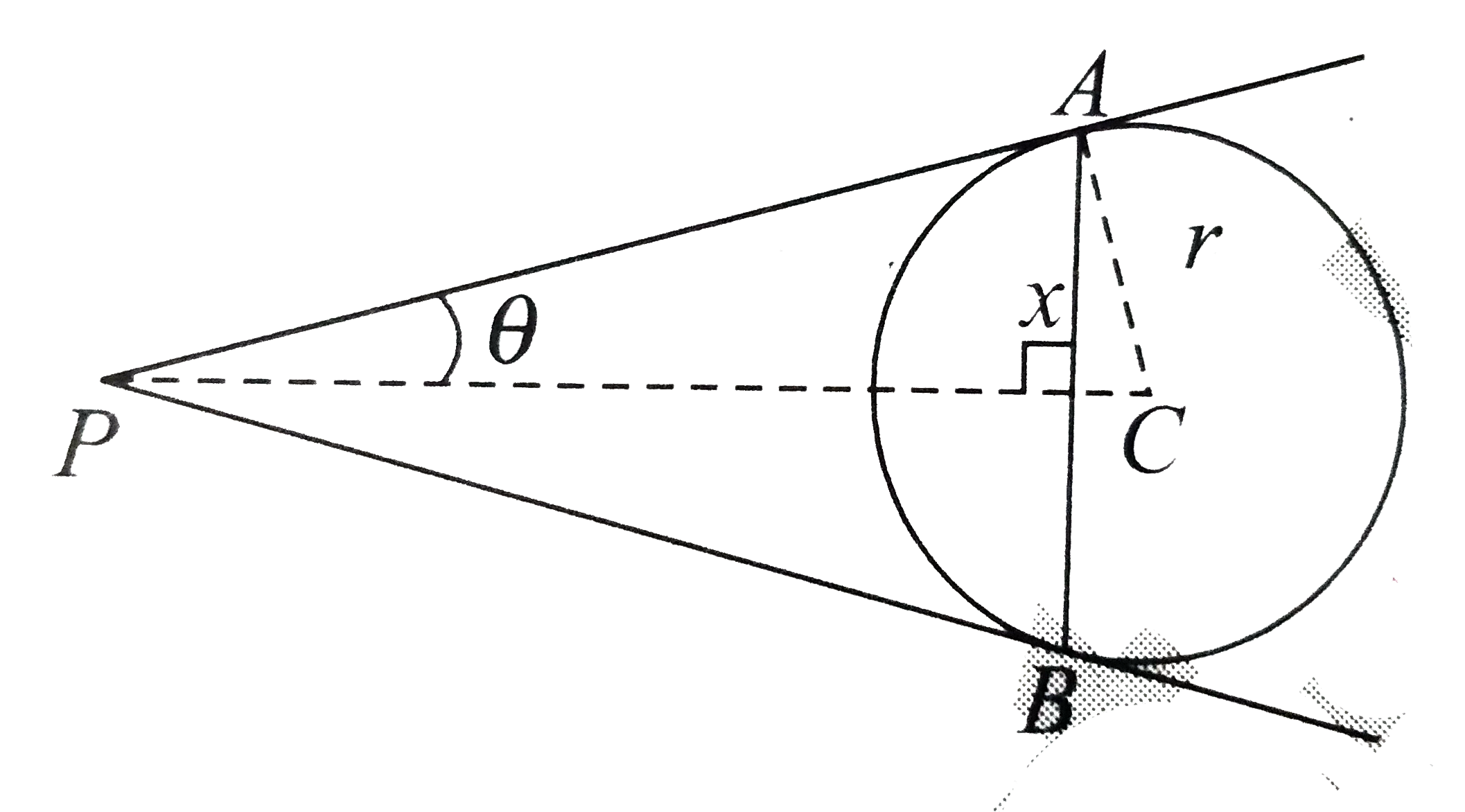
⇒cot2θ+1(PA)2=116
⇒PAsinθ=4=x⇒2x=8.
Topper's Solved these Questions
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - JEE Advanced (Single Correct Answer Type)
14 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Question Bank
30 Videos
Similar Questions
From a point P outside a circle with centre at C, tangents PA and PB are drawn such that 1(CA)2+1(PA)2=116, then fid the length of chord AB.
View SolutionFrom a point P outside a circle with centre O, tangents PA and PB are drawn to the circle. Prove that OP is the right bisector of the line segment AB.
View Solution
Knowledge Check
From a point P outside the circle with centre O, two tangents PA and PB are drawn to meet the circle at A and B respectively. If ∠APB=70∘, then ∠OAB is equal to :
केंद्र O वाले वृत्त के बाहर स्थित किसी बिंदु P से दो स्पर्श रेखाएं PA और PB खींची जाती हैं जो वृत्त से क्रमशः A और B मिलती हैं | यदि ∠APB=70∘ है, तो कोण OAB का मान ज्ञात करें |A35∘B65∘C45∘D55∘If tangents PA and PB are drawn from P(−1,2) to y2=4x then
AEquation of AB is y=x−1BLength of AB is 8CLength of AB is 4DEquation of AB is y=x+1From any arbitrary point P on the line +y = 4, tangents PA and PB are drawn to the circlex2+y2=8. Find the equation that satisfies the locus of the midpoint of AB.
Ax2+y2+2x+2y=0Bx2+y2−2x−2y=0Cx2+y2−2x+2y=0Dx2+y2+2x−2y=0
From a point P, two tangents PA and PB are drawn such that PA=9 cm and ∠APB=60∘. Find the length of chord AB.
View SolutionIf PA and PB are tangents from an outside point P such that PA=10cm and ∠APB=60o . Find the length of chord AB .
View SolutionFrom the point P(4,−4) tangents PA and PB are drawn to the circle x2+y2−6x+2y+5=0 whose centre is C then Length of AB
View SolutionIn the given figure, from the point P two tangents PA and PB are drawn to a circle with centre O and radius 5cm. From the point O, OC and OD are drawn parallel to PA and PB respectively. If the length of the chord AB is 5cm, then what is the value of (in degrees) of ∠COD ?
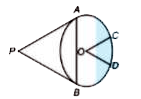
View SolutionAB is a chord of circle with centre O. At B, a tangent PB is drawn such that its length is 24 cm. The distance of P from the centre is 26 cm. If the chord AB is 16 cm, find its distance from the centre.
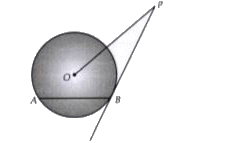
View Solution
