AB is a chord of $x^{2} + y^{2} = 4$ and P(1, 1) trisects AB. Then the length of the chord AB is (a) 1.5 units (c) 2.5 units (b) 2 units (d) 3 units

A

1.5 units

B

2 units

C

2.5 units

D

3 units

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

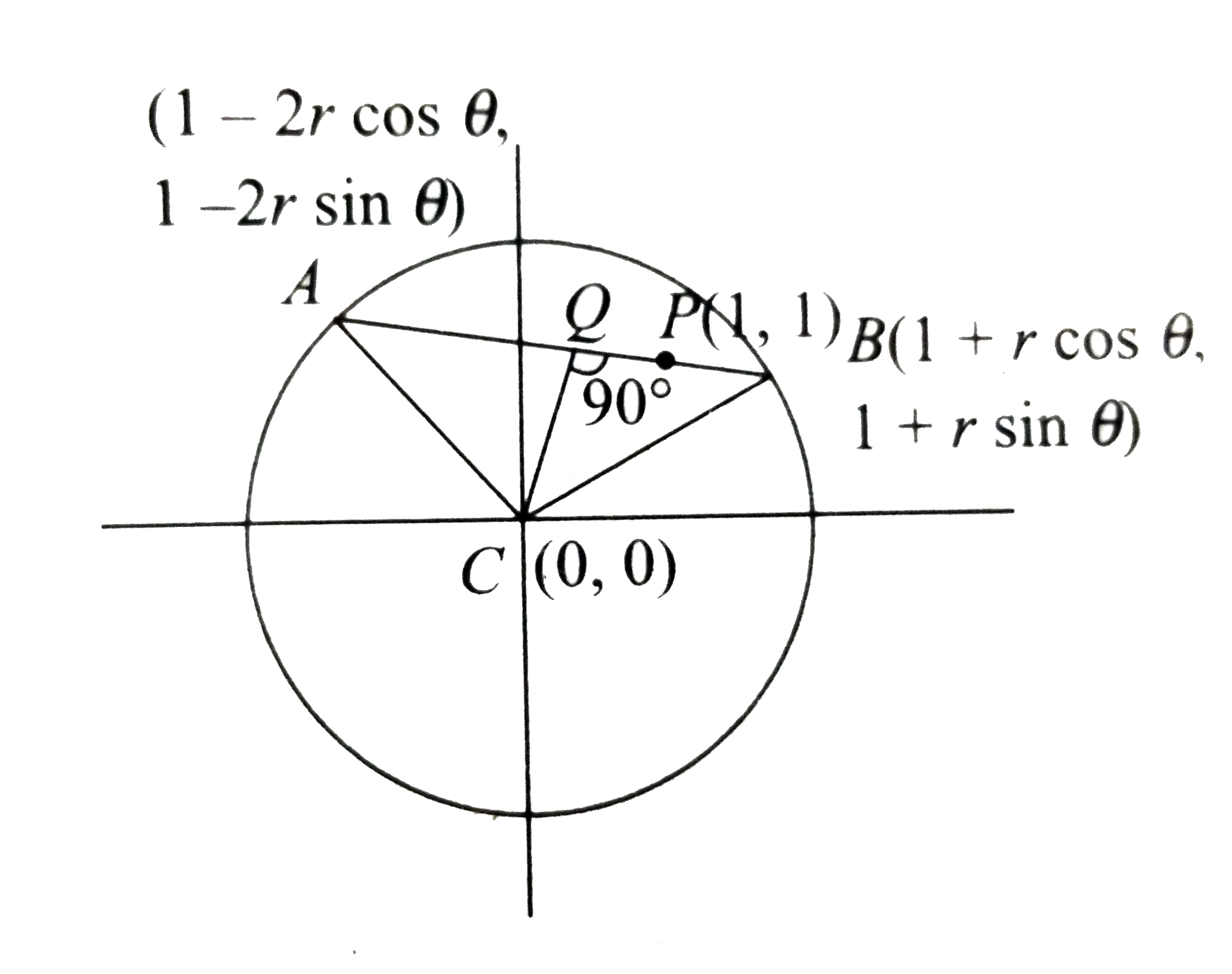
Given in $A P : A B = 2 : 1$
Let $A P = 2 r$ and $B P = r$
Using parametric equations
$A = (1 - 2 r cos θ, 1 - 2 r sin θ)$
$B = (1 + r cos θ, 1 + r sin θ)$
A lies on the circle $x^{2} + y^{2} = 4$
$\Rightarrow {(1 - 2 r cos θ)}^{2} + {(1 - 2 r sin θ)}^{2} = 4$ (1)
B lies on the circle $x^{2} + y^{2} = 4$
$\Rightarrow {(1 + r cos θ)}^{2} + {(1 + r sin θ)}^{2} = 4$ (2)
Solving (1) and (2), we get $r = 1$
$\Rightarrow A B = \sqrt{{(3 r cos θ)}^{2} + {(3 r sin θ)}^{2}} = 3 r = 3$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

CENGAGE-CIRCLES-Single Correct Answer Type

Home
Ask Doubt
Profile