if P,Q are two points on the line 3x+4y+15=0 such that OP=OQ=9 then the area of triangle OPQ is
18 sq. units
18√2 sq. units
27 sq. units
none of these
The correct Answer is:B
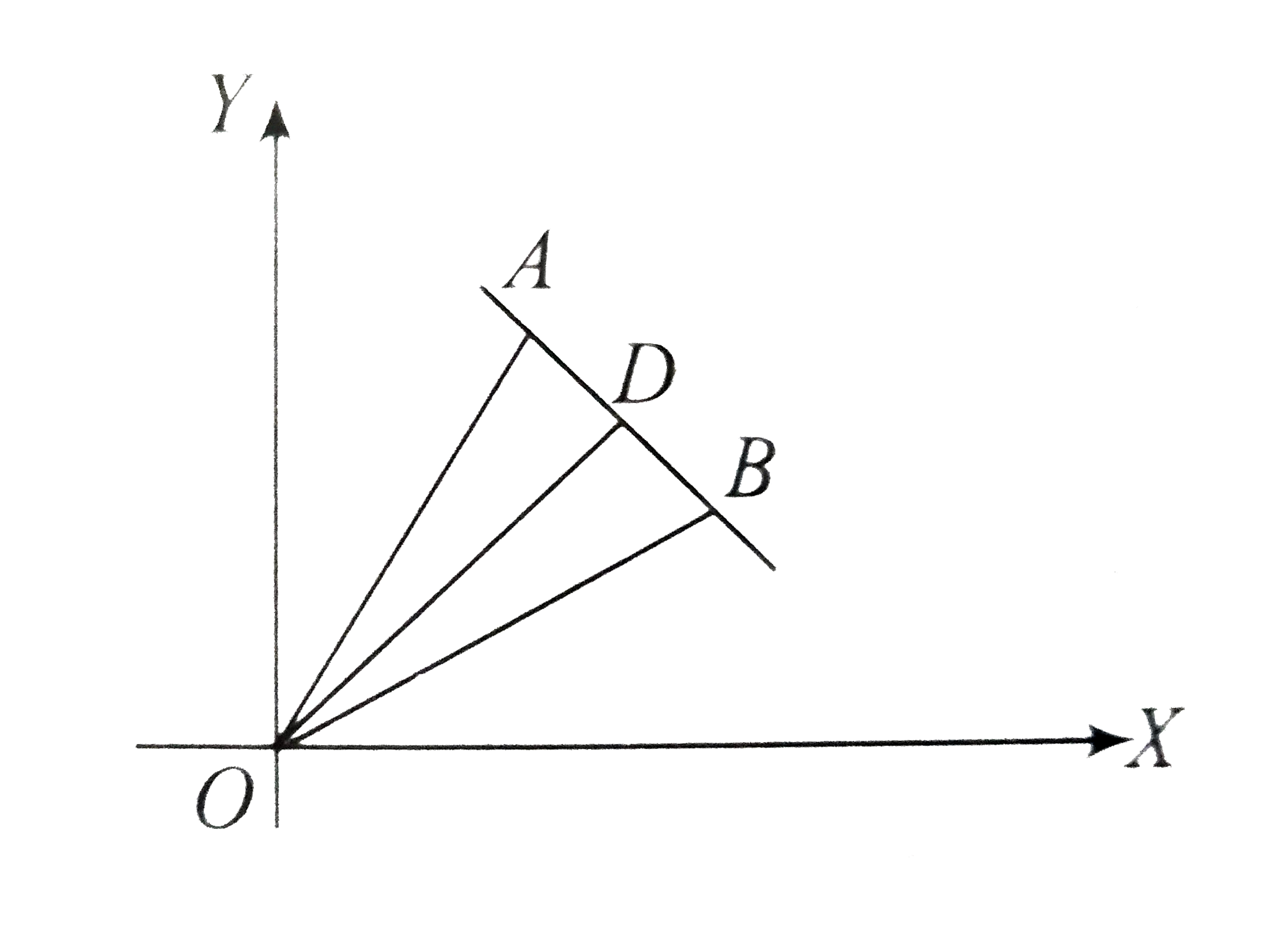
OA=OB=9,OD=15√25=3
∴AB=2AD=2√81−9=2√72=12√2
Hence Δ=12(3×12√2)=18√2 sq. units.
Topper's Solved these Questions
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Comprehension Type
3 Videos
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- STATISTICSBOOK - CENGAGECHAPTER - STATISTICSEXERCISE - JEE Previous Year
10 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - JEE Advanced Previous Year
4 Videos
Similar Questions
Knowledge Check
If P and Q are two points on the line 3x + 4y = - 15, such that OP = OQ = 9 units, the area of the triangle POQ will be
A18√2 sq unitsB3√2 sq unitsC6√2 sq unitsD15√2 sq unitsIf P and Q are two points on the line 3x + 4y = - 15, such that OP = OQ = 9 units, the area of the triangle POQ will be
A9√2B18√2C12√2DNoneLet P is a point on the line y+2x=2 and Q and R are two points on the line 3y+6x=3. If the triangle PQR is an equilateral triangle, then its area (in sq. units) is equal to
A115B15√3C13√5D12√15
If P be any point on the plane ln+my+nz=P and Q be a point on the line OP, such that (OP)(OQ)=P2 . The locus of point Q is
View Solutionlf from point P(4,4) perpendiculars to the straight lines 3x+4y+5=0 and y=mx+7 meet at Q and R area of triangle PQR is maximum, then m is equal to
View SolutionP and Q are two variable points on the axes of x and y respectively such that |OP| + |OQ|=a, then the locus of foot of perpendicular from origin on PQ is
View SolutionA straight line passing through the point (87, 33) cuts the positive direction of the coordinate axes at the point P and Q. If Q is the origin then the minimum area of the triangle OPQ is.
View SolutionConsider the lines y = 3x , y = 6x , y = 9
What is the area of the triangle formed by these lines ?
View Solution
