The equation of the diagonals of a rectangle are $y + 8 x - 17 = 0$ and $y - 8 x + 7 = 0$ . If the area of the rectangle is $8 s q u n i t s$ then find the sides of the rectangle

A

$x = 1$

B

$x + y = 1$

C

$y = 9$

D

$x - 2 y = 3$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, C

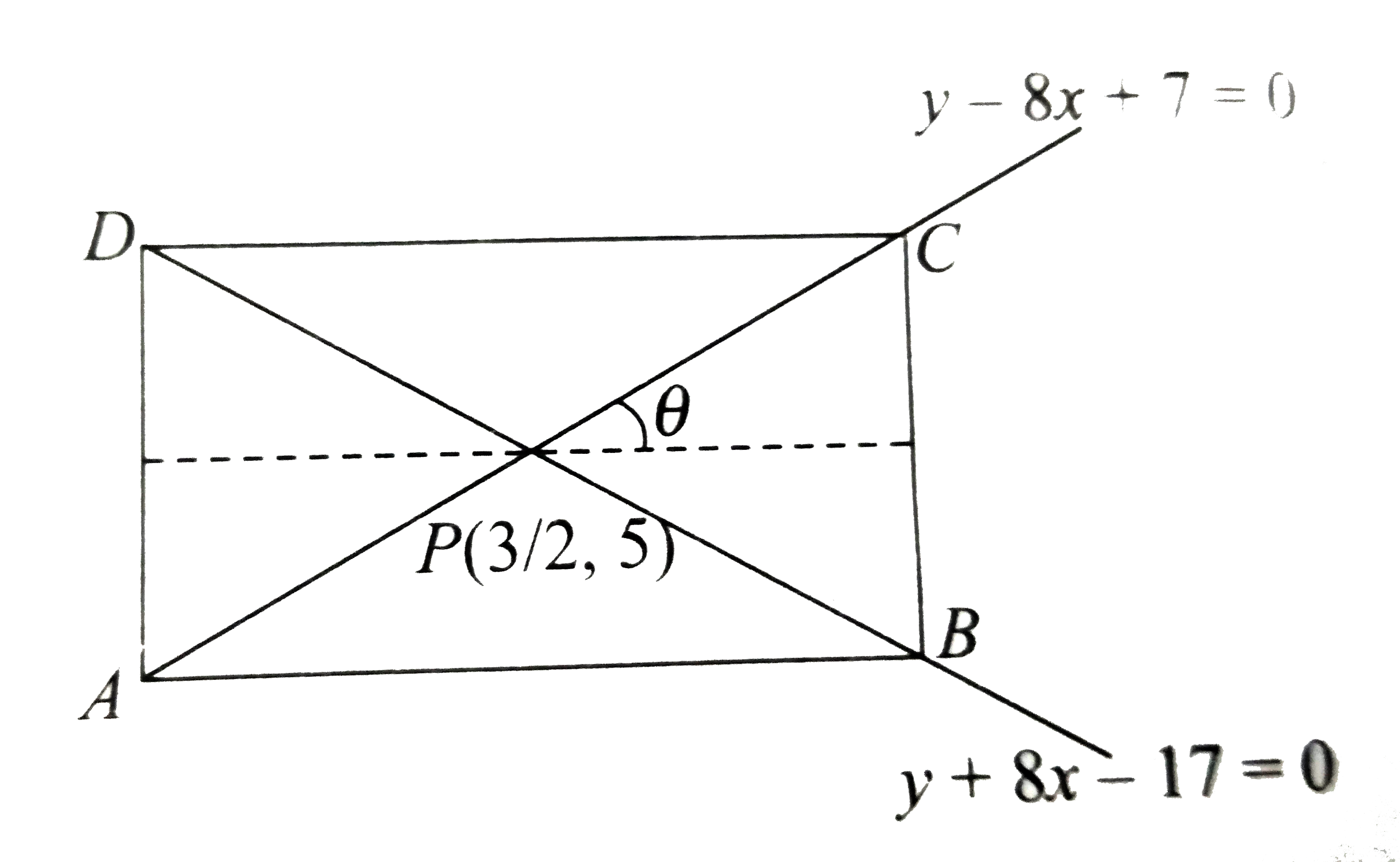
The intersection point of the given diagonals is $P \equiv (\frac{3}{2}, 5)$
Equation of angle bisectors of the diagonals are
$\frac{y + 8 x - 17}{\sqrt{65}} = \pm \frac{y - 8 x + 7}{\sqrt{65}}$
or $x = \frac{3}{2}$ and $y = 5$
Let the length of BC be a and that of CD be b.
Then $tan = \frac{a / 2}{b / 2} = \frac{a}{b} = 8$ .
Also $a b = 8$
$\Rightarrow a = 8, b = 1$ .
So equations of side are $y = 1, y = 9, x = 1$ and $x = 2$

|

Updated on:21/07/2023

Class 12 MATHS STRAIGHT LINE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If the diagonal of a rectangle is 17 cm long and its perimeter is 46 cm, the area of the rectangle is
A $100 c m^{2}$
B $110 c m^{2}$
C $120 c m^{2}$
D $150 c m^{2}$
Question 2 - Select One
The sides of a rectangle are given by $x = \pm a$ and $y = \pm b$ . The equation of the circle passing through the vertices of the rectangle is
A $x^{2} + y^{2} = a^{2}$
B $x^{2} + y^{2} = a^{2} + b^{2}$
C $x^{2} + y^{2} = a^{2} - b^{2}$
D ${(x - a)}^{2} + {(y - b)}^{2} = a^{2} + b^{2}$
Question 3 - Select One
A rectangle has an area of $144 c m^{2}$ . If the length is 7 cm more than the breadth of the rectangle. Find the sides of the rectangle.
A12 cm
B9 cm
C16 cm
D15 cm

CENGAGE-STRAIGHT LINE-Multiple Correct Answers Type

Home
Ask Doubt
Profile