If (a, b) be an end of a diagonal of a square and the other diagonal has the equation $x - y = a$ , then another vertex of the square can be

A

$(a - b, a)$

B

$(a, 0)$

C

$(0, - a)$

D

$(a + b, b)$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B, D

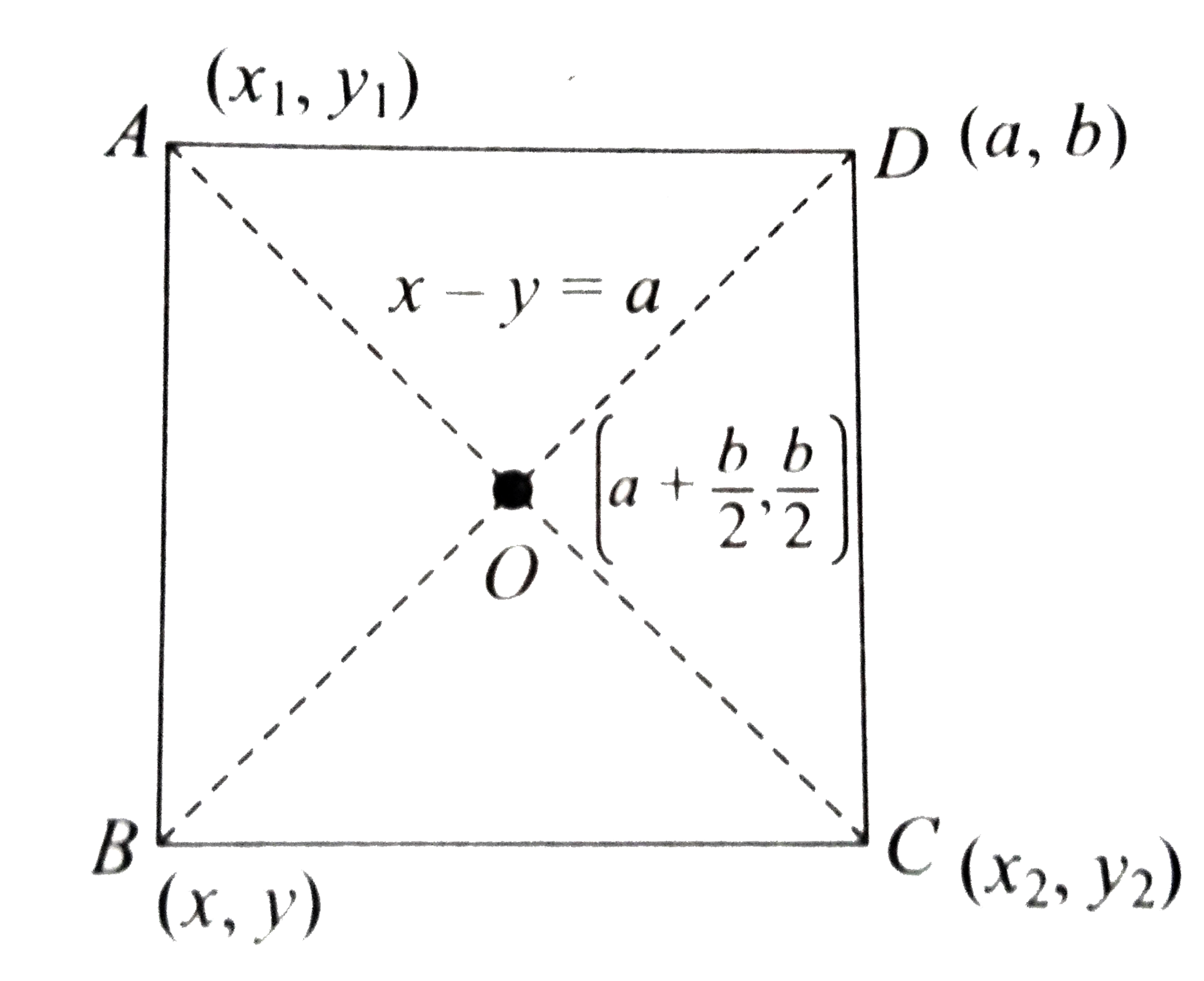
Diagonal AC is $x - y = a$
$∴$ Slope $B D = - 1$
Also BD passes through (a,b)
$∴$ Equation of BD is $x + y = a + b$
Solving, we get point $O \equiv (a + \frac{b}{2}, \frac{b}{2})$
$∴$ point $B \equiv (a + b, 0)$
$m_{A C} = 1 = tan θ$
$O A = O D = \frac{b}{\sqrt{2}}$
Using parametric form of straight line points A and C are given by
$(a + \frac{b}{2} \pm \frac{b}{\sqrt{2}} {cos 45}^{\circ}, \frac{b}{2} \pm \frac{b}{\sqrt{2}} {sin 45}^{\circ})$
or $A (a, 0)$ and $C (a + b, b)$

Updated on:21/07/2023

|

Class 12 MATHS STRAIGHT LINE

Topper's Solved these Questions

Similar Questions

Knowledge Check

The ratio of the area of a square to that of the square drawn on its diagonal is :
A $1 : \sqrt{2}$
B $1 : 2$
C $1 : 3$
D $1 : 4$

CENGAGE-STRAIGHT LINE-Multiple Correct Answers Type

Home
Ask Doubt
Profile