Let $A (a, 0) and B (b, 0)$ be fixed distinct points on the x-axis, none of which coincides with the $O (0, 0)$ , and let C be a point on the y-axis. Let L be a line through the $O (0, 0)$ and perpendicular to the line AC. The locus of the point of intersection of the lines L and BC if C varies along is (provided $c^{2} + a b \neq 0$ )

A

$\frac{x^{2}}{a} + \frac{y^{2}}{b} = x$

B

$\frac{x^{2}}{a} + \frac{y^{2}}{b} = y$

C

$\frac{x^{2}}{b} + \frac{y^{2}}{a} = x$

D

$\frac{x^{2}}{b} + \frac{y^{2}}{a} = y$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Equation of the line L is $y = \frac{a}{c} x$
As (h,k) lies on it, hence
$k = \frac{a}{c} h$ (i)
Now equation of BC
$\frac{x}{b} + \frac{y}{c} = 1$
(h,k) lies on it
$∴ \frac{h}{b} + \frac{k}{c} = 1$

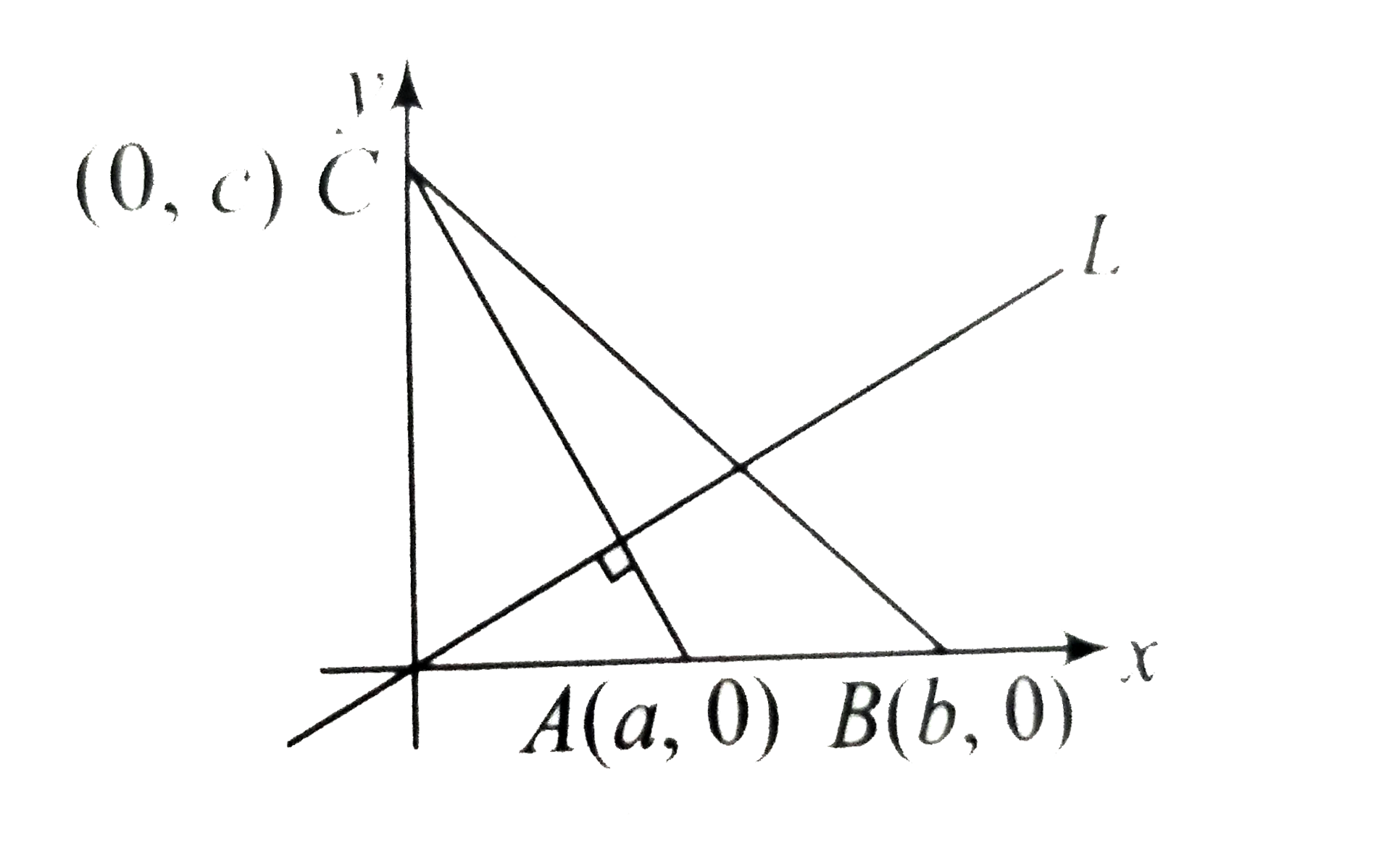
Substituting $c = \frac{a h}{k}$ in (ii) from (i)
$\frac{h^{2}}{h b} + \frac{k^{2}}{a h} = 1$
$∴$ Locus of P is $\frac{x^{2}}{b} + \frac{y^{2}}{a} = x$

Updated on:21/07/2023

|

Class 12 MATHS STRAIGHT LINE

Topper's Solved these Questions

Similar Questions

Knowledge Check

The line through the pont of intersection of lines $a x + b y + c = 0$ and $d x + b' y + c' = 0$ which is parallel to y-axis is
A $x (a b' - d' b) + (c b' - c' b) = 0$
B $x (a b' - a' b) + (c b' + c' b) = 0$
C $y (a b' - a' b) + (a c' - d' c) = 0$
Dnone
Let l be the line through $(0, 0)$ an tangent to the curve $y = x^{3} + x + 16 .$ Then the slope of l equal to :
A10
B11
C17
D13
A line L passeds through the points $(1, 1) and (2, 0)$ and another line L' passes through $(\frac{1}{2}, 0)$ and perpendicular to L. Then the area of the triangle formed by the lines L, L' and Y-axis is
A $\frac{15}{8}$
B $\frac{25}{4}$
C $\frac{25}{8}$
D $\frac{25}{16}$

CENGAGE-STRAIGHT LINE-Multiple Correct Answers Type

Home
Ask Doubt
Profile