There is a Young's double-slit experiment set-up completely dipped in water. Assume that the refractive index of water is μ1. One of the slits is covered with a thin film of thickness t and refractive index μ2. What will be the optical path difference at the centre of screen ?
|(μ2−μ1)t|
|(μ2−1)t|
∣∣∣(μ2μ1−1)t∣∣∣
∣∣∣(μ1μ2−1)t∣∣∣
The correct Answer is:C
To find the optical path difference at the center of the screen in a Young's double-slit experiment setup completely immersed in water, with one slit covered by a thin film, we can follow these steps:
1. Understanding the Setup:
- The Young's double-slit experiment consists of two slits (let's call them slit 1 and slit 2) that emit light waves. The entire setup is submerged in water, which has a refractive index denoted as μ1.
- One of the slits (say slit 1) is covered with a thin film of thickness t and refractive index μ2.
2. Optical Path Difference (OPD) Concept:
- The optical path difference is defined as the difference in the effective distance traveled by light from the two slits to the screen.
- When light travels through different media, the effective distance is modified by the refractive index of the medium.
3. Calculating the OPD for the Thin Film:
- For the light passing through the thin film, the optical path length is given by the formula:
Optical Path Length=Refractive Index×Thickness
- In this case, the effective optical path length for the light passing through the thin film is:
OPLfilm=μ2⋅t
4. Calculating the OPD in Water:
- The light from slit 2, which does not pass through any thin film, travels through water, and its optical path length is:
OPLwater=μ1⋅0=0
- Thus, the optical path difference (OPD) at the center of the screen, where the two waves meet, is given by:
OPD=OPLfilm−OPLwater=μ2⋅t−0=μ2⋅t
5. Relative Refractive Index:
- Since the entire setup is in water, we need to consider the relative refractive index of the thin film with respect to the surrounding water. The relative refractive index μrelative is given by:
μrelative=μ2μ1
- Therefore, the optical path difference can be expressed as:
OPD=(μ2μ1−1)t
Final Result:
The optical path difference at the center of the screen is:
OPD=(μ2μ1−1)t
- The Young's double-slit experiment consists of two slits (let's call them slit 1 and slit 2) that emit light waves. The entire setup is submerged in water, which has a refractive index denoted as μ1.
- One of the slits (say slit 1) is covered with a thin film of thickness t and refractive index μ2.
- The optical path difference is defined as the difference in the effective distance traveled by light from the two slits to the screen.
- When light travels through different media, the effective distance is modified by the refractive index of the medium.
- For the light passing through the thin film, the optical path length is given by the formula:
Optical Path Length=Refractive Index×Thickness
- In this case, the effective optical path length for the light passing through the thin film is:
OPLfilm=μ2⋅t
- The light from slit 2, which does not pass through any thin film, travels through water, and its optical path length is:
OPLwater=μ1⋅0=0
- Thus, the optical path difference (OPD) at the center of the screen, where the two waves meet, is given by:
OPD=OPLfilm−OPLwater=μ2⋅t−0=μ2⋅t
- Since the entire setup is in water, we need to consider the relative refractive index of the thin film with respect to the surrounding water. The relative refractive index μrelative is given by:
μrelative=μ2μ1
- Therefore, the optical path difference can be expressed as:
OPD=(μ2μ1−1)t
The optical path difference at the center of the screen is:
OPD=(μ2μ1−1)t
Topper's Solved these Questions
- WAVE OPTICALBook:MODERN PUBLICATIONChapter:WAVE OPTICALExercise:OBJECTIVE TYPE QUESTIONS (B. MULTIPLE CHOICE QUESTIONS) -AIPMT/NEET & OTHER STATE BOARDS FOR MEDICAL ENTRANCE
Explore 10 Videos
- WAVE OPTICALBook:MODERN PUBLICATIONChapter:WAVE OPTICALExercise:OBJECTIVE TYPE QUESTIONS (JEE (MAIN) & OTHER STATE BOARDS FOR ENGINEERING ENTRANCE)
Explore 22 Videos
- WAVE OPTICALBook:MODERN PUBLICATIONChapter:WAVE OPTICALExercise:Revision Exercises (Numerical Problems)
Explore 31 Videos
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS Book:MODERN PUBLICATIONChapter:SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS Exercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 12 Videos
Similar Questions
Two parallel rays are travelling in a medium of refractive index μ1=43 . One of the rays passes through a parallel glass slab of thickness t and refractive index μ2=32 The path difference between the two rays due to the glass slab will be
View SolutionIn Young's double slit experiment the fringe width is 4mm .If the experiment is shifted to water of refractive index 43 the fringe width becomes (in mm)
View Solution
Knowledge Check
If entire Young's double-slit experiment set-up is immersed in water, then
Afringe width will remain unaffectedBfringe width will increaseCfringe width will decreaseDexperiment cannot be performed in water.In Young's double-slit experiment, if both the slits are covered by a thin transparent sheet of thickness t and refractive index n, the optical path difference between the two interfering waves
Aincreases by (n -1) tBdecrease by (n -1) tCchanges by Dd (n-1) tDis not affected.A YDSE is conducted in water (μ1) as shown in figure. A glass plate of thickness t and refractive index μ2 is placed in the path of S2. The optical path difference at O is
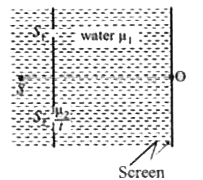 A(μ2−1)tB(μ1−1)tC(μ2μ1−1)tD(μ2−μ1)t
A(μ2−1)tB(μ1−1)tC(μ2μ1−1)tD(μ2−μ1)t
In the YDSE shown the two slits are covered with thin sheets having thickness t&2t and refractive index 2μand μ .Find the position (y) of central maxima.

View SolutionTwo parallel rays are travelling in a medium of refractive index μ1=4/3. One of the rays passes through a parallel glass slab of thickness t and refractive index μ2=3/2. The path difference between the two rays due to the glass slab will be
View SolutionYoung's double slit experiment is conducted in a liquid of refractive index μ1 as shown in figure. A thin transparent slab of refractive index μ2 is placed in front of the slit s2. The magnitude of optical path difference at 'O' is
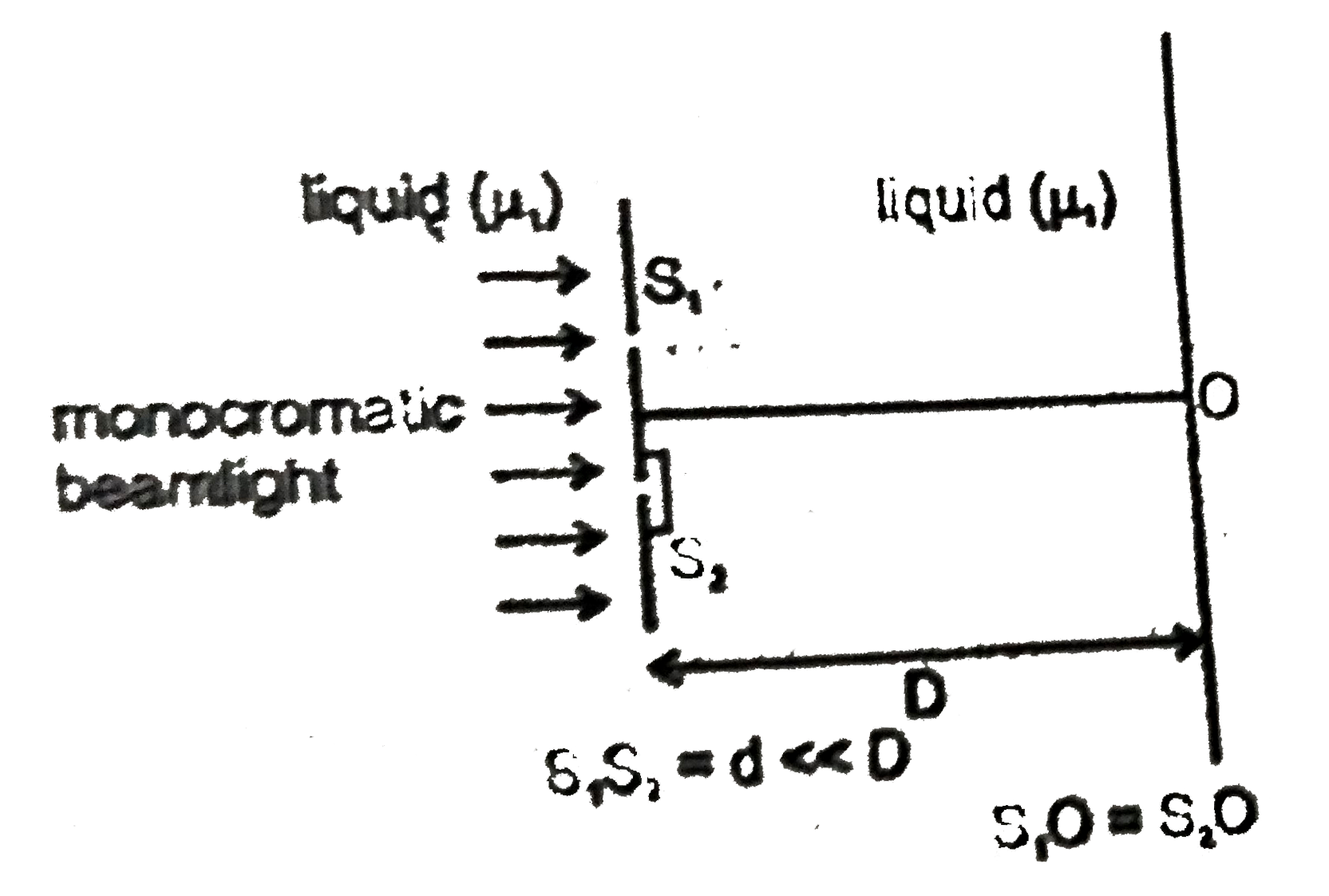
View SolutionIn double slit experiment fringes are obtained using light of wavelength 4800Å One slit is covered with a thin glass film of refractive index. 1.4 and another slit is covered by a film of same thickness but refractive index 1.7. By doing so, the central fringe is shifted to fifth bright fringe in the original pattern. The thickness of glass film is
View SolutionWith a monochromatic light, the fringe-width obtained in a Young’s double slit experiment is 0.133 cm. The whole set- up is immersed in water of refractive index 1.33, then the new fringe-width is
View Solution

