A cube of side b has a charge q at each of its vertices. Determine the potential and electric field due to this charge array at the center of the cube.
From the figure the distance of centre from each vertex in the cube can be calculated as:
HC2=HF2+CF2
⇒HC2=(√2b)2+b2=3b2
⇒HC=√3b
∴HO=√32b
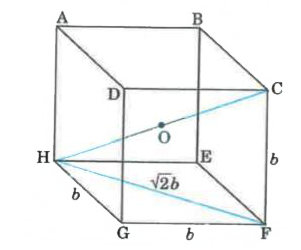
Potential at the centre O can be calculated as:
V=8×14πε0qr=4q√3πε0b
Net electric field at the centre of the cube is zero due to symmetry.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:NCERT FILE Solved (Additional Exercises) (Answer carefully)
Explore 7 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:NCERT FILE Solved (Additional Exercises) (Answer the following)
Explore 4 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:NCERT FILE Solved (Textbook Exercise)
Explore 11 Videos
- ELECTROMAGNETIC WAVESBook:MODERN PUBLICATIONChapter:ELECTROMAGNETIC WAVESExercise:CHAPTER PRACTICE TEST
Explore 14 Videos
- MAGNETISM AND MATTERBook:MODERN PUBLICATIONChapter:MAGNETISM AND MATTERExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 16 Videos
Similar Questions
A cube of side b has a charge g at each of its vertices. Determine the potential and electric field due to this charge array at the centre of the cube.
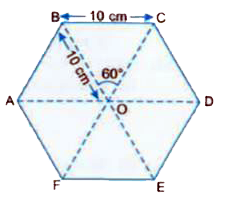
View SolutionA regular hexagon of side 10 cm has a charge 5μC at each of its vertices. Calculate the potential at the centre of the hexagon.
View Solution
Knowledge Check
A hexagon of side 'a' has a charge 'q' at each of its vertices. The electric field at the centre of hexagon is
A0B14π∈0.qa2C14π∈0.6qa2D14π∈0.6q2a2A hexagon of side 8 cm has a charge 4μC at each of its vertices. The potential at the centre of the hexagon is
A2.7×106VB7.2×1011VC2.5×1012VD3.4×104VA cube of side 'a' has point charges +Q located at each of its vertices except at the origin where the charge is -Q. The electric field at the centre of cube is :
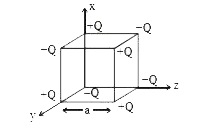 A−Q3√3πε0a2(ˆx+ˆy+ˆz)B−2Q3√3πε0a2(ˆx+ˆy+ˆz)C2Q3√3πε0a2(ˆx+ˆy+ˆz)DQ3√3πε0a2(ˆx+ˆy+ˆz)
A−Q3√3πε0a2(ˆx+ˆy+ˆz)B−2Q3√3πε0a2(ˆx+ˆy+ˆz)C2Q3√3πε0a2(ˆx+ˆy+ˆz)DQ3√3πε0a2(ˆx+ˆy+ˆz)
A regular hexagon of side 10 cm has a charge 5μC at each of its vertices. Calculate the potential at the center of the hexagon.
View SolutionA cube of side a has a charge q at each of its vertices. The potential energy of the system, of charges is "(Kq^(2))/(a)((12)/(z)+6sqrt(x)+(4)/(sqrt(y)))." Then find "x+y+z".
View SolutionGiven a cube with point charges q on each of its vertices. Calculate the force exerted on any of the charges due to rest of the 7 charges.
View SolutionThe total electric flux through a cube when a charge 8q is placed at one comer of the cube is
View SolutionThe total electric flux through a cube when a charge 8q is placed at one corner of the cube is
View Solution

